题目内容
如图,斜三棱柱ABC—A1B1C1的底面是直角三角形,AC⊥CB,
∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
(1)求证EF//平面A1ACC1;
(2)求EF与侧面A1ABB1所成的角;
(3)求二面角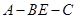 的大小的余弦值.
的大小的余弦值.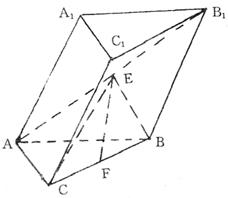
∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
(1)求证EF//平面A1ACC1;
(2)求EF与侧面A1ABB1所成的角;
(3)求二面角
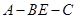 的大小的余弦值.
的大小的余弦值.
(1)见解析;(2)EF与平面A1ABB1所成的角为30°;
(3)二面角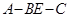 的大小为余弦值
的大小为余弦值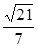 .
.
(3)二面角
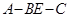 的大小为余弦值
的大小为余弦值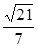 .
.(1)本题的关键是证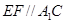 ,连接A1B,A1C,显然EF是三角形A1CB的中位线,问题得证.
,连接A1B,A1C,显然EF是三角形A1CB的中位线,问题得证.
(2)先做出线面角是解本小题的关键.作FG⊥AB交AB于G,连EG ∵侧面A1ABB1⊥平面ABC且交线是AB ∴FG⊥平面A1ABB1,∴∠FEG是EF与平面A1ABB1所成的角
(3)取AB的中点M,可以证明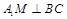 ,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,然后利用向量法求二面角即可.
,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,然后利用向量法求二面角即可.
证明: (1)∵A1ABB1是菱形,E是AB1中点,∴E是A1B中点,连A1C ,∵F是BC中点,
∴EF∥A1C
∵ A1C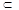 平面A1ACC1,EF
平面A1ACC1,EF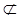 平面A1ACC1, ∴EF//平面A1ACC1
平面A1ACC1, ∴EF//平面A1ACC1
(2)作FG⊥AB交AB于G,连EG ∵侧面A1ABB1⊥平面ABC且交线是AB ∴FG⊥平面A1ABB1,∴∠FEG是EF与平面A1ABB1所成的角
由AB=a,AC⊥BC,∠ABC=45°,得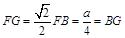 由AA1=AB=a,∠A1AB=60°,
由AA1=AB=a,∠A1AB=60°,
得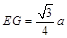
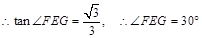 ∴ EF与平面A1ABB1所成的角为30°
∴ EF与平面A1ABB1所成的角为30°
(3)取AB的中点M,可以证明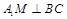 ,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,不难求得平面ABE的一个法向量为
,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,不难求得平面ABE的一个法向量为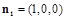 ,平面BEC的一个法向量为
,平面BEC的一个法向量为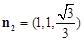 ,
,
∴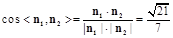 ,∴二面角
,∴二面角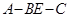 的大小为余弦值
的大小为余弦值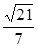 .
.
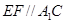 ,连接A1B,A1C,显然EF是三角形A1CB的中位线,问题得证.
,连接A1B,A1C,显然EF是三角形A1CB的中位线,问题得证.(2)先做出线面角是解本小题的关键.作FG⊥AB交AB于G,连EG ∵侧面A1ABB1⊥平面ABC且交线是AB ∴FG⊥平面A1ABB1,∴∠FEG是EF与平面A1ABB1所成的角
(3)取AB的中点M,可以证明
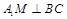 ,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,然后利用向量法求二面角即可.
,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,然后利用向量法求二面角即可. 证明: (1)∵A1ABB1是菱形,E是AB1中点,∴E是A1B中点,连A1C ,∵F是BC中点,
∴EF∥A1C
∵ A1C
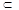 平面A1ACC1,EF
平面A1ACC1,EF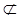 平面A1ACC1, ∴EF//平面A1ACC1
平面A1ACC1, ∴EF//平面A1ACC1 (2)作FG⊥AB交AB于G,连EG ∵侧面A1ABB1⊥平面ABC且交线是AB ∴FG⊥平面A1ABB1,∴∠FEG是EF与平面A1ABB1所成的角
由AB=a,AC⊥BC,∠ABC=45°,得
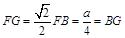 由AA1=AB=a,∠A1AB=60°,
由AA1=AB=a,∠A1AB=60°,得
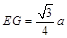
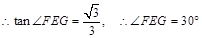 ∴ EF与平面A1ABB1所成的角为30°
∴ EF与平面A1ABB1所成的角为30°(3)取AB的中点M,可以证明
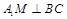 ,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,不难求得平面ABE的一个法向量为
,以BC为y轴,以MC为x轴,MA1为z轴建立空间直角坐标系,不难求得平面ABE的一个法向量为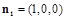 ,平面BEC的一个法向量为
,平面BEC的一个法向量为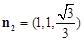 ,
,∴
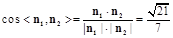 ,∴二面角
,∴二面角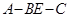 的大小为余弦值
的大小为余弦值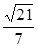 .
.
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
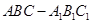 中,
中,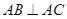 ,
,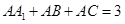 ,
,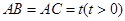 ,
,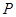 是侧棱
是侧棱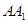 上的动点.
上的动点.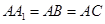 时,求证:
时,求证: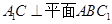 ;
; 的平面角的余弦值为
的平面角的余弦值为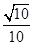 ,试求实数
,试求实数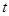 的值.
的值.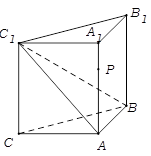
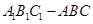 中,
中, 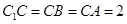 ,
, .
. 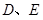 分别为棱
分别为棱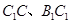 的中点.
的中点.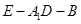 的平面角的余弦值;
的平面角的余弦值;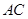 上是否存在一点
上是否存在一点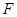 ,使得
,使得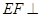 平
平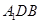 ?
?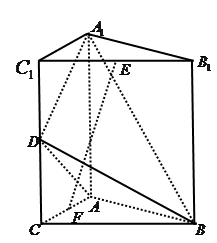
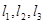 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )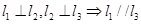
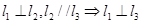
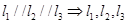 共面
共面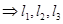 共面
共面
 中,底面
中,底面 为矩形,平面
为矩形,平面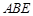 ,
,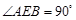 ,
,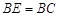 ,
,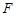 为
为 的中点,
的中点,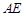 ∥平面
∥平面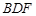 ;(2)平面
;(2)平面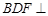 平面
平面 .
.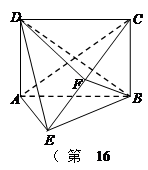
 ,直线
,直线 ,则下列四个命题:①
,则下列四个命题:①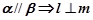 ;②
;② ;③
;③ ;④
;④ .其中正确的是( ).
.其中正确的是( ). 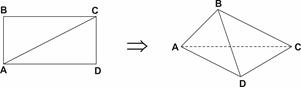
 为平行四边形,
为平行四边形,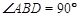 ,
,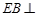 平面
平面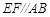 ,
,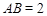 ,
, ,
,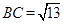 ,且
,且 是
是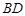 的中点.
的中点. 平面
平面 ;
;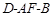 的大小;
的大小;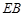 上是否存在一点
上是否存在一点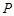 ,使得
,使得 与
与 所成的角为
所成的角为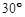 ? 若存在,求出
? 若存在,求出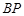 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.