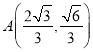题目内容
【题目】在平面直角坐标系xOy中，已知圆
，圆心
，点E在直线
上，点P满足
，
，点P的轨迹为曲线M．
（1）求曲线M的方程．
（2）过点N的直线l分别交M于点A、B，交圆N于点C、D（自上而下），若
、
、
成等差数列，求直线l的方程．
【答案】（1）
；（2）
．
【解析】
（1）设
，由
，得
，代入
化简得：，所以点P的轨迹曲线M的方程为：；
（2）由
、
、
成等差数列，得弦长
，对直线l的斜率分情况讨论，当斜率不存在时，
，不符合题意；当斜率存在时，设
，
，直线l的方程为：
，联立，利用韦达定理可求得k的值，从而得到直线l的方程．
（1）设，由，得，
则
，
，
，
，
由，得
，即
，
化简得：，所以点P的轨迹曲线M的方程为：；
（2）由、、成等差数列，得
，
所以弦长，
①当斜率不存在时，直线l的方程为：
，
交点
，
，此时，不符合题意；
②当斜率存在时，设直线l的方程为：，，，
联立方程
，消去y得：
，
∴
，
，
显然
恒成立，
由抛物线的定义可知，
，
∴
，解得：
，∴直线l的方程为．
练习册系列答案
快捷英语周周练系列答案
相关题目
