题目内容
【题目】已知椭圆![]() 过点
过点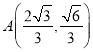 .其左、右两个焦点分别为
.其左、右两个焦点分别为![]() 、
、![]() ,短轴的一个端点为
,短轴的一个端点为![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() :
:![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
,![]() ,且
,且![]() 为坐标原点.若
为坐标原点.若![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,由![]() 可得
可得![]() ,将点
,将点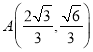 代入椭圆方程,结合椭圆中
代入椭圆方程,结合椭圆中![]() 的关系,即可求得椭圆的标准方程.
的关系,即可求得椭圆的标准方程.
(2)设![]() ,
,![]() ,联立直线与椭圆方程,化简后由韦达定理表示出
,联立直线与椭圆方程,化简后由韦达定理表示出![]() ,
,![]() .由
.由![]() 解得
解得![]() ;由
;由![]() ,可结合平面向量数量积的坐标运算求得
,可结合平面向量数量积的坐标运算求得![]() ,表示出
,表示出![]() ,利用换元法可令
,利用换元法可令![]() ,即可化简为关于
,即可化简为关于![]() 的表达式,结合对勾函数的图像与性质即可求得
的表达式,结合对勾函数的图像与性质即可求得![]() 的最大值.
的最大值.
(1)由题意得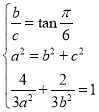 ,解得
,解得![]() ,
,
所以椭圆的方程为![]() .
.
(2)设![]() ,
,![]() .
.
则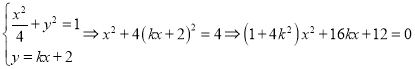 ,
,
∴![]() ,
,![]() .
.
由![]() ,
,
化简可得![]() ,解得
,解得![]() .①
.①
由![]() ,得
,得![]() ,
,
所以![]() .
.
又![]() ,
,
∴![]()
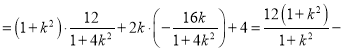
![]() ,所以
,所以![]() .②
.②
综合①②可知![]() .
.
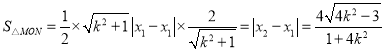
令![]()
则![]() ,
,![]() ,所以
,所以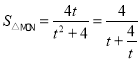 ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以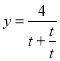 在
在![]() 上单调递减,
上单调递减,
当![]() ,即
,即![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

练习册系列答案
相关题目
【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x/万件 | 10 | 11 | 13 | 12 | 8 | 6 |
利润y/万元 | 22 | 25 | 29 | 26 | 16 | 12 |
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程![]() x+
x+![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?