Question

【题目】学校举办的集体活动中，设计了如下有奖闯关游戏：参赛选手按第一关、第二关、第三关的顺序依次闯关，若闯关成功，分别获得1分、2分、3分的奖励，游戏还规定，当选手闯过一关后，可以选择得到相应的分数，结束游戏；也可以选择继续闯下一关，若有任何一关没有闯关成功，则全部分数都归零，游戏结束。设选手甲第一关、第二关、第三关的概率分别为，，，选手选择继续闯关的概率均为，且各关之间闯关成功互不影响

（I）求选手甲第一关闯关成功且所得分数为零的概率

(II)设该学生所得总分数为X,求X的分布列与数学期望

Answer 1

【答案】（Ⅰ）；（Ⅱ）见解析.

【解析】分析：（Ⅰ）设甲“第一关闯关成功且所得分数为零”为事件A，“第一关闯关成功第二关闯关失败”为事件A1，“前两关闯关成功第三关闯关失败”为事件A2，由A1，A2互斥，能求出选手甲第一关闯关成功且所得学豆为零的概率．

（Ⅱ）X所有可能的取值为0，1，3，6，分别求出相应的概率，由此能求出X的分布列和数学期望．

详解：（Ⅰ）设甲“第一关闯关成功且所得分数为零”为事件，“第一关闯关成功第二关闯关失败”为事件，“前两关闯关成功第三关闯关失败”为事件，则，互斥，

， ，

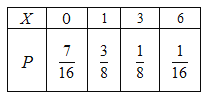
（Ⅱ）所有可能的取值为0,1,3,6

，

，

，

所以，的分布列为：

.