Question

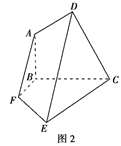
【题目】已知在三棱锥中，底面,,，是的中点，是线段上的一点，且，连接.

（l）求证：平面；

（2）求直线与平面所成角的正切值．

Answer 1

【答案】（1）见解析；（2）

【解析】分析：（1）求出AE=4．由勾股定理得BE=2．推导出AC是Rt△ABE的斜边BE上的中线，从而C是BE的中点．进而直线CD是Rt△ABE的中位线，CD∥AB．由此能证明CD∥平面PAB；

（2）以为原点，直线分别为轴，建立如下图所示的空间直角坐标系，求出直线的方向向量与平面的法向量，带入公式即可.

详解：（1）证明：因为，所以.

又，，

所以在中，由勾股定理，得.

因为，

所以是的斜边上的中线.

所以是的中点.

又因为是的中点,

所以直线是的中位线，所以.

又因为平面，平面，所以平面.

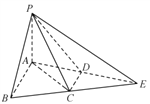
（2）解：以为原点，直线分别为轴，建立如下图所示的空间直角坐标系：

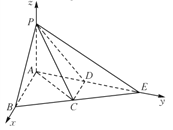
因为，且分别是的中点，

所以，.所以点，，，，.

所以，，.

设平面的法向量为，则

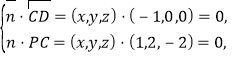由得得

所以令，得平面的一个法向量为；

设直线与平面所成角的大小为，则.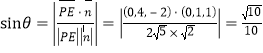

又，所以根据同角三角函数的基本关系，得.

所以.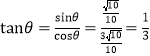

故直线与平面所成角的正切值为.