题目内容
【题目】已知函数 ![]() 且函数y=f(x)图象上点(1,f(1))处的切线斜率为0.
且函数y=f(x)图象上点(1,f(1))处的切线斜率为0.
(1)试用含有a的式子表示b,并讨论f(x)的单调性;
(2)对于函数图象上的不同两点A(x1 , y1),B(x2 , y2)如果在函数图象上存在点M(x0 , y0),(x0∈(x1 , x2))使得点M处的切线l∥AB,则称AB存在“跟随切线”.特别地,当 ![]() 时,又称AB存在“中值跟随切线”.试问:函数f(x)上是否存在两点A,B使得它存在“中值跟随切线”,若存在,求出A,B的坐标,若不存在,说明理由.
时,又称AB存在“中值跟随切线”.试问:函数f(x)上是否存在两点A,B使得它存在“中值跟随切线”,若存在,求出A,B的坐标,若不存在,说明理由.
【答案】
(1)解:f(x)的定义域为(0,+∞),
∵f′(x)= ![]() ﹣ax+b=0,
﹣ax+b=0,
∴b=a﹣1,∴f′(x)= ![]() ﹣ax+a﹣1=﹣
﹣ax+a﹣1=﹣ ![]() ,
,
当f′(x)>0时,∵x>0,a>0,解得0<x<1,
当f′(x)<0时,∵x>0,a>0,解得x>1,
∴当f(x)在(0,1)上单调递增,在(1,+∞)上单调递减
(2)解:假设函数f(x)的图象上存在两点A(x1,y1),B(x2,y2),使得AB存在“中值跟随切线”,
则kAB= ![]() =
= ![]() ﹣
﹣ ![]() +a﹣1,
+a﹣1,
f′( ![]() )=
)= ![]() ﹣
﹣ ![]() +a﹣1,
+a﹣1,
又kAB=f′( ![]() )得
)得 ![]() =
= ![]() ,
,
∴ln ![]() =t,(t>1),则lnt=2﹣
=t,(t>1),则lnt=2﹣ ![]() ,(t>1),此式表示有大于1的实数根,
,(t>1),此式表示有大于1的实数根,
令h(t)=lnt+ ![]() ﹣2(t>1),则h′(t)=
﹣2(t>1),则h′(t)= ![]() >0
>0
∴h(t)是(1,+∞)上的增函数,
∴h(t)>h(1)=0,与lnt=2﹣ ![]() ,(t>1)有大于1的实数根相矛盾,
,(t>1)有大于1的实数根相矛盾,
∴函数f(x)的图象上不存在两点A(x1,y1),B(x2,y2),使得AB存在“中值跟随切线”
【解析】(1)根据对数函数的定义求得函数的定义域,根据f(x)的解析式求出f(x)的导函数,利用f′(1)=0,代入导函数化简即可得到a与b的关系式,用a表示出b;然后分别令导函数大于0和小于0得到关;(2)假设函数f(x)的图象上存在两点A(x1 , y1),B(x2 , y2),使得AB存在“中值相依切线”,根据斜率公式求出直线AB的斜率,利用导数的几何意义求出直线AB的斜率,它们相等,再通过构造函数,利用导数研究函数的单调性和最值即可证明结论.于x的不等式,求出不等式的解集即可得到相应的x的范围即分别为函数的递增和递减区间.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 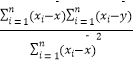 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.