题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{2-|x-2|,(0≤x<4)}\\{{2}^{x-2}-3,(4≤x≤6)}\end{array}\right.$,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的取值范围是( )| A. | [0,1) | B. | [1,4] | C. | [1,6] | D. | [0,1]∪[3,8] |
分析 由已知中函数f(x)=$\left\{\begin{array}{l}{2-|x-2|,(0≤x<4)}\\{{2}^{x-2}-3,(4≤x≤6)}\end{array}\right.$,可得当0≤x1<4≤x2≤6时,若f(x1)=f(x2),则x1∈[1,3],进而得到x1•f(x2)的表达式,数形结合,可得x1•f(x2)的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}2-|x-2|,(0≤x≤4)\\{2}^{x-2}-3,(4≤x≤6)\end{array}\right.$的图象如下图所示: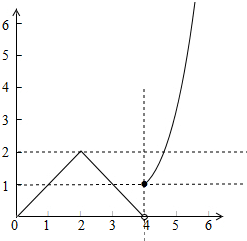
当0≤x1<4≤x2≤6时,若f(x1)=f(x2),
则x1∈[1,3],
∴x1•f(x2)=x1•f(x1)=x1•(2-|x1-2|)=$\left\{\begin{array}{l}{x}_{1}^{2},1≤{x}_{1}<2\\{-x}_{1}^{2}+4{x}_{1},2≤{x}_{1}<3\end{array}\right.$,
其图象如下图所示: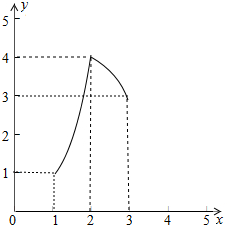
即x1•f(x2)的范围是[1,4].
故选:B
点评 本题考查的知识点是分段函数的图象和性质,分段函数的应用,数形结合思想,难度中档.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=PB,AC⊥BC,AB=4,PC=6,则三棱锥P-ABC的外接球O的表面积为( )
| A. | $\frac{81π}{2}$ | B. | 41π | C. | 32$\sqrt{2}$π | D. | 32π |
15.复数1+$\sqrt{3}$i的三角形式是( )
| A. | cos$\frac{π}{3}$+isin$\frac{π}{3}$ | B. | 2(cos$\frac{π}{3}$+isin$\frac{π}{3}$) | C. | cos$\frac{π}{6}$+isin$\frac{π}{6}$ | D. | 2(cos$\frac{π}{6}$+isin$\frac{π}{6}$) |
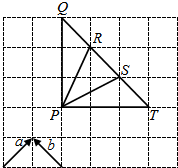 如图所示,下列结论正确的是( )
如图所示,下列结论正确的是( )