题目内容
(本小题满分14分)
动圆G与圆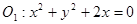 外切,同时与圆
外切,同时与圆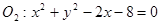 内切,设动圆圆心G的轨迹为
内切,设动圆圆心G的轨迹为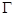 。
。
(1)求曲线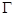 的方程;
的方程;
(2)直线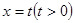 与曲线
与曲线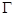 相交于不同的两点
相交于不同的两点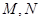 ,以
,以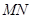 为直径作圆
为直径作圆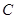 ,若圆C与
,若圆C与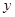 轴相交于两点
轴相交于两点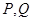 ,求
,求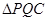 面积的最大值;
面积的最大值;
(3)设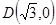 ,过
,过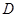 点的直线
点的直线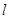 (不垂直
(不垂直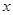 轴)与曲线
轴)与曲线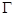 相交于
相交于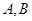 两点,与
两点,与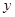 轴交于点
轴交于点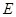 ,若
,若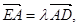
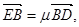 试探究
试探究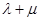 的值是否为定值,若是,求出该定值,若不是,请说明理由。
的值是否为定值,若是,求出该定值,若不是,请说明理由。
动圆G与圆
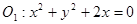 外切,同时与圆
外切,同时与圆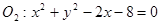 内切,设动圆圆心G的轨迹为
内切,设动圆圆心G的轨迹为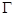 。
。(1)求曲线
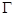 的方程;
的方程;(2)直线
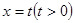 与曲线
与曲线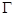 相交于不同的两点
相交于不同的两点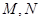 ,以
,以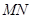 为直径作圆
为直径作圆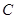 ,若圆C与
,若圆C与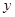 轴相交于两点
轴相交于两点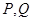 ,求
,求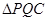 面积的最大值;
面积的最大值;(3)设
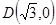 ,过
,过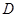 点的直线
点的直线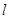 (不垂直
(不垂直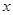 轴)与曲线
轴)与曲线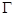 相交于
相交于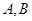 两点,与
两点,与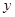 轴交于点
轴交于点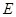 ,若
,若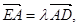
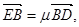 试探究
试探究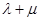 的值是否为定值,若是,求出该定值,若不是,请说明理由。
的值是否为定值,若是,求出该定值,若不是,请说明理由。(1)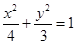 ;(2)
;(2)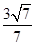 ;(3)
;(3)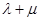
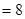 。
。
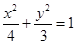 ;(2)
;(2)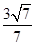 ;(3)
;(3)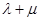
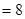 。
。本试题主要是考查了椭圆方程的求解,以及直线与椭圆方程的位置关系的综合运用。
(1) 利用圆圆位置关系,得到圆心距与半径的关系式,从而得到点的轨迹方程。
(2) 设出直线方程与椭圆方程联立,结合韦达定理得到结论。
(3) 设直线与椭圆联立方程组,利用过圆心得到垂直关系,结合韦达定理得到结论。
解:(1)设圆G的半径为r,依题意得: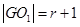 ,
,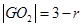
所以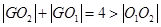 ,所以G点轨迹是以
,所以G点轨迹是以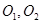 为焦点的椭圆,
为焦点的椭圆,
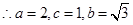
所以曲线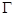 的方程是
的方程是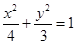 ………… 4分
………… 4分
(2)依题意,圆心为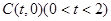 .
.
由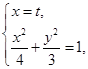 得
得 . ∴ 圆
. ∴ 圆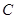 的半径为
的半径为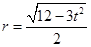 .
.
∵ 圆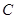 与
与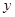 轴相交于不同的两点
轴相交于不同的两点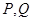 ,且圆心
,且圆心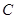 到
到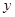 轴的距离
轴的距离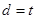 ,
,
∴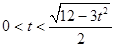 ,即
,即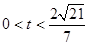 .
.
∴ 弦长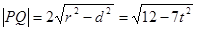 ∴
∴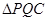 的面积
的面积
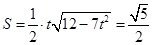
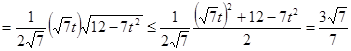
当且仅当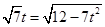 即
即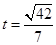 时,等号成立,
时,等号成立,
所以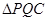 面积的最大值是
面积的最大值是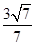 ………………… 8分
………………… 8分
(3)依题意,直线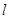 的斜率存在,设
的斜率存在,设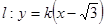 ,
,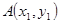 ,
,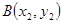 ,则
,则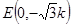
由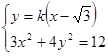 消
消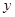 得:
得: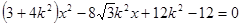 ,
,
则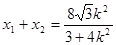 ①
① 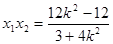 ②
②
由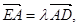 得
得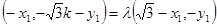 ,所以
,所以
又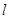 不垂直
不垂直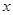 轴,所以
轴,所以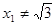 ,故
,故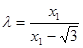 ,同理
,同理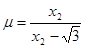 ;
;
所以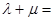
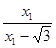
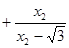 =
=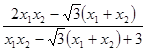 ,
,
将①②代入上式得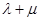
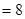 ………………… 14分
………………… 14分
(1) 利用圆圆位置关系,得到圆心距与半径的关系式,从而得到点的轨迹方程。
(2) 设出直线方程与椭圆方程联立,结合韦达定理得到结论。
(3) 设直线与椭圆联立方程组,利用过圆心得到垂直关系,结合韦达定理得到结论。
解:(1)设圆G的半径为r,依题意得:
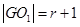 ,
,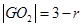
所以
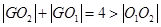 ,所以G点轨迹是以
,所以G点轨迹是以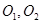 为焦点的椭圆,
为焦点的椭圆,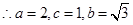
所以曲线
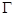 的方程是
的方程是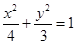 ………… 4分
………… 4分(2)依题意,圆心为
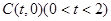 .
.由
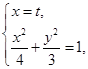 得
得 . ∴ 圆
. ∴ 圆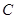 的半径为
的半径为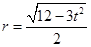 .
. ∵ 圆
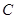 与
与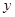 轴相交于不同的两点
轴相交于不同的两点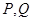 ,且圆心
,且圆心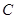 到
到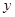 轴的距离
轴的距离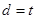 ,
,∴
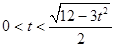 ,即
,即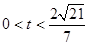 .
. ∴ 弦长
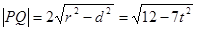 ∴
∴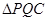 的面积
的面积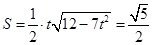
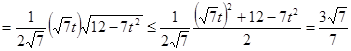
当且仅当
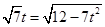 即
即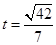 时,等号成立,
时,等号成立,所以
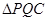 面积的最大值是
面积的最大值是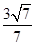 ………………… 8分
………………… 8分(3)依题意,直线
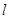 的斜率存在,设
的斜率存在,设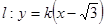 ,
,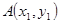 ,
,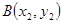 ,则
,则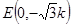
由
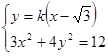 消
消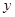 得:
得: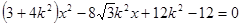 ,
,则
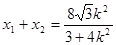 ①
① 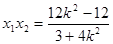 ②
②由
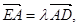 得
得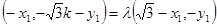 ,所以
,所以
又
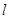 不垂直
不垂直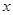 轴,所以
轴,所以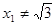 ,故
,故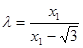 ,同理
,同理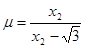 ;
;所以
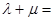
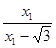
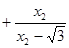 =
=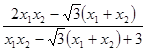 ,
,将①②代入上式得
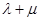
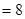 ………………… 14分
………………… 14分
练习册系列答案
相关题目
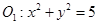 与⊙
与⊙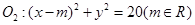 相交于
相交于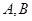 两点,且两圆在点
两点,且两圆在点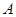 处的切线互相垂直,则线段
处的切线互相垂直,则线段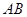 的长度是
的长度是 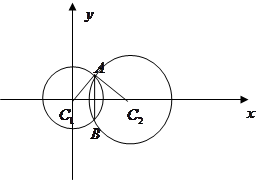

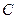 与圆
与圆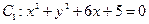 外切,同时与圆
外切,同时与圆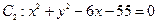 内切.
内切.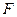 的方程;
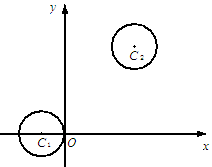
的方程;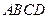 中(如图),
中(如图),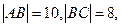
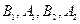 分别是矩形四边的中点,
分别是矩形四边的中点,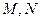 分别是
分别是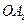 (其中
(其中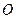 是坐标系原点)
是坐标系原点)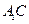 的中点,直线
的中点,直线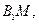
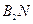 的交点为
的交点为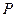 ,证明点
,证明点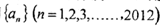 ,圆
,圆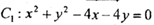 ,
,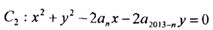 ,若圆C2平分圆C1的周长,则
,若圆C2平分圆C1的周长,则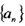 的所有项的和为.
的所有项的和为.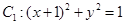 ,圆
,圆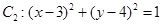 .
.
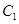 的直线
的直线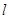 被圆
被圆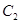 截得的弦长为
截得的弦长为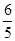 ,求直线
,求直线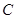 同时平分圆
同时平分圆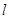 上的两点,且
上的两点,且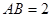 .两个半径相等的动圆分别与
.两个半径相等的动圆分别与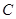 是这两个圆的公共点,则圆弧
是这两个圆的公共点,则圆弧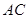 ,
,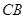 与线段
与线段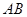 围成图形面积
围成图形面积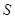 的取值范围是
的取值范围是 

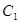 :
: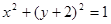 ,⊙
,⊙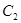 :
: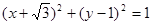 ;坐标平面内的点
;坐标平面内的点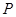 满足:存在过点
满足:存在过点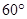 的直线
的直线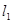 和
和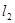 ,它们分别与⊙
,它们分别与⊙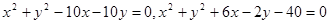 ,
,