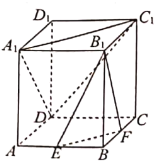
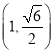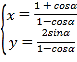ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥–£ќ™ЅЋЅЋљвЄя“ї–¬…ъ «Јс‘Є“в≤ќЉ”Њь—µ£ђЋжїъµч≤йЅЋ80√ы–¬…ъ£ђµ√µљ»зѕ¬2°Ѕ2Ѕ–Ѕ™±н
‘Є“в | ≤ї‘Є“в | ЇѕЉ∆ | |
ƒ– | x | 5 | M |
≈Ѓ | y | z | 40 |
ЇѕЉ∆ | N | 25 | 80 |
£®1£©–і≥ц±н÷–x£ђy£ђz£ђM£ђNµƒ÷µ£ђ≤Ґ≈–ґѕ «Јс”–99.9%µƒ∞—ќ’»ѕќ™‘Є“в≤ќЉ”Њь—µ”л–‘±р”–єЎ£ї
£®2£©‘Џ±їµч≤йµƒ≤ї‘Є“в≤ќЉ”Њь—µµƒ—І…ъ÷–£ђЋжїъ≥й≥ц3»Ћ£ђЉ«’в3»Ћ÷–ƒ–…ъµƒ»Ћ эќ™¶ќ£ђ«у¶ќµƒЈ÷≤ЉЅ–ЇЌ э—І∆ЏЌы£Ѓ
≤ќњЉєЂ љ£Ї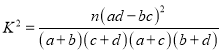
Єљ£Ї
P£®K2°Ёk0£© | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
°Њір∞Є°њ(1)M£љ40£ђx£љ35£ђz£љ20£ђy£љ20£ђN£љ55£ђ”–99.9%µƒ∞—ќ’»ѕќ™‘Є“в≤ќЉ”÷Њ‘Є’яћо±®≈а—µ”л–‘±р”–єЎ£Ѓ(2)Ј÷≤ЉЅ–Љыѕкљв£ђE(¶ќ£©![]() .
.
°Њљвќц°њ
£®1£©ЄщЊЁ±нЄс÷– эЊЁ£ђЉіњ…«уµ√x£ђy£ђz£ђM£ђNµƒ÷µ£ђ‘ўЉ∆Ћг![]() £ђљбЇѕ≤ќњЉ±нЄсЉіњ…„ч≥ц≈–ґѕ£ї
£ђљбЇѕ≤ќњЉ±нЄсЉіњ…„ч≥ц≈–ґѕ£ї
£®2£©Ѕ–≥ц¶ќµƒ»°÷µ£ђЄщЊЁє≈µдЄ≈–ЌЄ≈¬ Љ∆ЋгєЂ љ«уµ√Ј÷≤ЉЅ–£ђ‘ўЄщЊЁЈ÷≤ЉЅ–Љ∆Ћг э—І∆ЏЌыЉіњ….
£®1£©”…±нЄс эЊЁњ…÷™£Ї
M£љ80©Б40£љ40£ђ
x£љ40©Б5£љ35£ђ
z£љ25©Б5£љ20£ђ
y£љ40©Б20£љ20£ђ
N£љ80©Б25£љ55£ђ
°яK2![]() 13.09£Њ10.828£ђ
13.09£Њ10.828£ђ
°а”–99.9%µƒ∞—ќ’»ѕќ™‘Є“в≤ќЉ”÷Њ‘Є’яћо±®≈а—µ”л–‘±р”–єЎ£Ѓ
£®2£©‘Џ±їµч≤йµƒ≤ї‘Є“в≤ќЉ”Њь—µµƒ—І…ъ÷–£ђЋжїъ≥й≥ц3»Ћ£ђ
Љ«’в3»Ћ÷–ƒ–…ъµƒ»Ћ эќ™¶ќ£ђ‘т¶ќµƒњ…ƒ№»°÷µќ™0,1,2,3£ђ
P£®¶ќ£љ0£©![]() £ђ
£ђ
P£®¶ќ£љ1£©![]() £ђ
£ђ
P£®¶ќ£љ2£©![]() £ђ
£ђ
P£®¶ќ£љ3£©![]() £ђ
£ђ
°а¶ќµƒЈ÷≤ЉЅ–ќ™£Ї
¶ќ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E£®¶ќ£©![]() £Ѓ
£Ѓ