题目内容
14. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-$\sqrt{3}$,0),过点F的直线交椭圆与A,B两点,当直线AB垂直x轴时,|AB|=$\frac{a}{2}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-$\sqrt{3}$,0),过点F的直线交椭圆与A,B两点,当直线AB垂直x轴时,|AB|=$\frac{a}{2}$.(1)求该椭圆方程;
(2)若斜率存在且不为0的动线段AB的中点为G,AB的垂直平分线与x轴和y轴分别交于D,E两点,O是坐标原点(如图所示),记△GFD的面积为S1,△OED的面积为S2,求$\frac{{S}_{1}{S}_{2}}{{{S}_{1}}^{2}+{{S}_{2}}^{2}}$的取值范围.
分析 (1)根据椭圆的左焦点F坐标及|AB|=$\frac{a}{2}$,利用椭圆的定义求出a与b的值,即可确定出椭圆方程;
(2)设出直线AB解析式,及A与B的坐标,联立直线与椭圆方程,消去y得到关于x的一元二次方程,利用韦达定理表示出G坐标,再设出D坐标,根据DG与AB垂直,EG与AB垂直,利用两直线垂直时斜率乘积为-1表示出D的横坐标与B纵坐标,根据直角三角形FGD与直角三角形EOD相似,得到面积之比等于相似比的平方,求出所求式子的范围即可.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-$\sqrt{3}$,0),|AB|=$\frac{a}{2}$,
∴|AF|=$\frac{b}{a}$$\sqrt{{a}^{2}-3}$=$\frac{a}{4}$(由椭圆性质得$\frac{2{b}^{2}}{a}$=$\frac{a}{2}$),
∵a2=b2+3,
∴a2=4,b2=1,
则椭圆方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)根据条件可得直线AB的斜率一定存在且不为零,设直线AB解析式为y=k(x+$\sqrt{3}$),
并设A(x1,y2),B(x2,y2),
联立得$\left\{\begin{array}{l}{y=k(x+\sqrt{3})}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y得:(4k2+1)x2+8$\sqrt{3}$k2x+12k2-4=0,
∴$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{4\sqrt{3}{k}^{2}}{4{k}^{2}+1}$,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{\sqrt{3}k}{4{k}^{2}+1}$,即G(-$\frac{4\sqrt{3}{k}^{2}}{4{k}^{2}+1}$,$\frac{\sqrt{3}k}{4{k}^{2}+1}$),
设D(xD,0),由DG⊥AB,EG⊥AB,得到$\frac{\frac{\sqrt{3}k}{4{k}^{2}+1}}{-\frac{4\sqrt{3}{k}^{2}}{4{k}^{2}+1}-{x}_{D}}$•k=-1,$\frac{\frac{\sqrt{3}k}{4{k}^{2}+1}-{y}_{B}}{-\frac{4\sqrt{3}{k}^{2}}{4{k}^{2}+1}}$•k=-1,
整理得:xD=-$\frac{3\sqrt{3}{k}^{2}}{4{k}^{2}+1}$,yB=-$\frac{3\sqrt{3}k}{4{k}^{2}+1}$,
∵Rt△FGD∽Rt△EOD,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{F{D}^{2}}{D{E}^{2}}$=$\frac{3({k}^{2}+1)^{2}}{(1+4{k}^{2})^{2}}$•$\frac{(1+4{k}^{2})^{2}}{27(1+{k}^{2}){k}^{2}}$=$\frac{{k}^{2}+1}{9{k}^{2}}$=$\frac{1}{9}$+$\frac{1}{9{k}^{2}}$>$\frac{1}{9}$,
设$\frac{{S}_{1}}{{S}_{2}}$=t,则t>$\frac{1}{9}$,即$\frac{{S}_{1}{S}_{2}}{{{S}_{1}}^{2}+4{{S}_{2}}^{2}}$=$\frac{1}{t+\frac{4}{t}}$,
∴$\frac{{S}_{1}{S}_{2}}{{{S}_{1}}^{2}+4{{S}_{2}}^{2}}$=$\frac{1}{t+\frac{4}{t}}$≤$\frac{1}{4}$,且$\frac{{S}_{1}{S}_{2}}{{{S}_{1}}^{2}+4{{S}_{2}}^{2}}$>0,
则$\frac{{S}_{1}{S}_{2}}{{{S}_{1}}^{2}+4{{S}_{2}}^{2}}$的范围为(0,$\frac{1}{4}$].
点评 此题考查了直线与圆锥曲线的关系,椭圆的标准方程,以及椭圆的简单性质,熟练掌握椭圆的简单性质是解本题第一问的关键.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
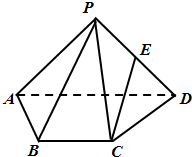 如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.
如图,四棱锥P-ABCD中,PA⊥PD,AD⊥CD,PA=PD,AD∥BC,AB=AD=2BC=2,E是棱PD的中点,设二面角P-AD-B的值为θ.