题目内容
已知数列 ,满足
,满足
(I)求证:数列 均为等比数列;
均为等比数列;
(Ⅱ)求数列 的通项公式
的通项公式 ;
;
(Ⅲ)求证: .
.
 ,满足
,满足
(I)求证:数列
 均为等比数列;
均为等比数列;(Ⅱ)求数列
 的通项公式
的通项公式 ;
;(Ⅲ)求证:
 .
.(I)详见试题解析;(Ⅱ) ;(Ⅲ)详见试题解析;.
;(Ⅲ)详见试题解析;.
 ;(Ⅲ)详见试题解析;.
;(Ⅲ)详见试题解析;.试题分析:(I)将已知式变形成
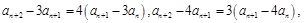 从而得
从而得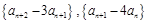 都是等比数列;(Ⅱ)由(I)
都是等比数列;(Ⅱ)由(I)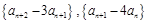 都是等比数列,可得
都是等比数列,可得 消去
消去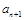 即得数列
即得数列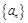 的通项公式;(Ⅲ)
的通项公式;(Ⅲ)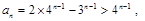 故
故 因而只要证
因而只要证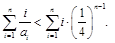 利用错位相减法求和:
利用错位相减法求和: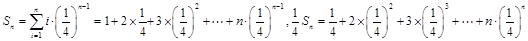 .最后利用放缩法证明不等式.
.最后利用放缩法证明不等式. 试题解析:(I)证明:
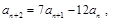 即
即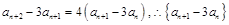 是首项为
是首项为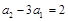 公比为
公比为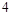 的等比数列. 2分
的等比数列. 2分又
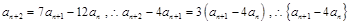 是首项为
是首项为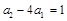 公比为
公比为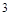 的等比数列. 4分
的等比数列. 4分(Ⅱ)解:由(I)知
 故
故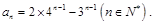 8分
8分(Ⅲ)证明:
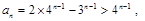 故
故 9分
9分则
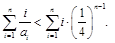
设
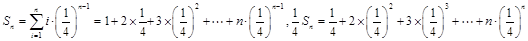 .
.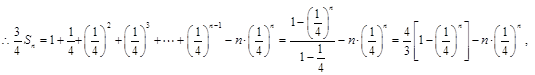
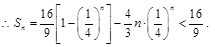 12分
12分故
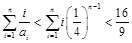 . 13分
. 13分
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
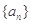 的前n项和为构成数列
的前n项和为构成数列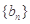 ,数列
,数列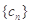 .
.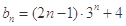 ,则
,则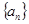 的各项均为正数,其前
的各项均为正数,其前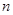 项和为
项和为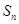 ,且
,且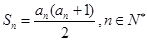 .
.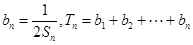 ,求证:
,求证: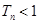 ;
;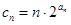 ,
,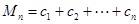 ,求
,求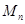 .
.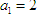 ,点
,点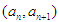 在函数
在函数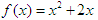 的图象上,其中
的图象上,其中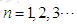
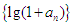 是等比数列,并求数列
是等比数列,并求数列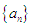 的通项公式;
的通项公式;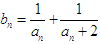 ,求数列
,求数列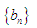 的前
的前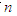 项和
项和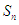 .
.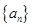 中,
中,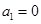 ,
,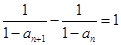 ,设
,设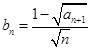 ,记
,记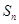 为数列
为数列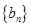 的前
的前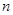 项和,则
项和,则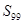 = .
= .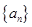 的前n项的和为
的前n项的和为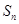 ,且
,且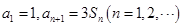 ,则
,则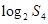 等于_ _
等于_ _ ,则其前n项和Sn=________.
,则其前n项和Sn=________.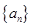 的前
的前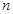 项和为
项和为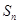 ,且
,且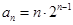 ,则
,则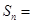 ______________.
______________.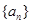 ,
,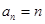 ,则数列
,则数列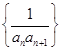 的前10项和为( )
的前10项和为( )


