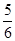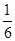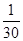题目内容
已知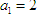 ,点
,点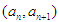 在函数
在函数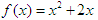 的图象上,其中
的图象上,其中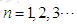
(1)证明:数列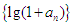 是等比数列,并求数列
是等比数列,并求数列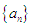 的通项公式;
的通项公式;
(2)记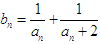 ,求数列
,求数列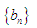 的前
的前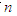 项和
项和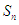 .
.
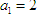 ,点
,点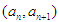 在函数
在函数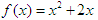 的图象上,其中
的图象上,其中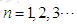
(1)证明:数列
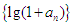 是等比数列,并求数列
是等比数列,并求数列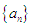 的通项公式;
的通项公式;(2)记
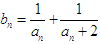 ,求数列
,求数列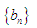 的前
的前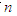 项和
项和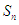 .
.(1)证明详见解析; 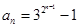 ;(2)
;(2) 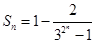
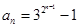 ;(2)
;(2) 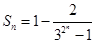
试题分析:(1)把点(an,an+1)代入f(x)=x2+2x中,整理可得递推公式an+1+1=(an+1)2,两边取常用对数,整理可证
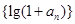 是公比为2,a1=2的等比数列,然后由数列
是公比为2,a1=2的等比数列,然后由数列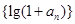 的通项公式可推出数列{an}的通项公式.(2)由已知递推公式an+1=an2+2an变形整理得
的通项公式可推出数列{an}的通项公式.(2)由已知递推公式an+1=an2+2an变形整理得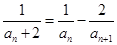 ,代入
,代入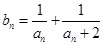 中,整理可得
中,整理可得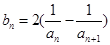 最后利用裂项法求数列的前n项和Sn.
最后利用裂项法求数列的前n项和Sn.试题解析:(Ⅰ)由已知
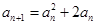 ,
, 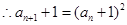
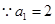
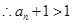 ,两边取对数得
,两边取对数得  ,即
,即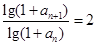
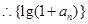 是公比为2的等比数列.
是公比为2的等比数列. 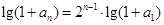
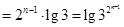
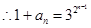 (*)
(*) 由(*)式得
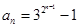
(2)
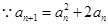
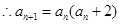

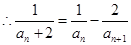
又
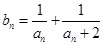
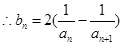
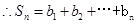
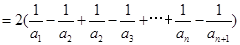
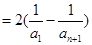
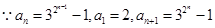
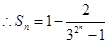 .
. 
练习册系列答案
相关题目
 的前
的前 项和
项和 ,函数
,函数 对
对 有
有 ,数列
,数列 满足
满足
 .
. 满足
满足 ,
,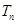 是数列
是数列 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立,求
恒成立,求 ,满足
,满足
 均为等比数列;
均为等比数列; 的通项公式
的通项公式 ;
; .
. 满足
满足 ,数列
,数列 满足
满足 .
. 项和
项和 .
.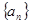 的前
的前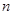 项和为
项和为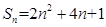 ,数列
,数列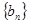 的首项
的首项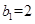 ,且点
,且点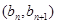 在直线
在直线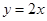 上.
上.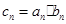 ,求数列
,求数列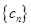 的前
的前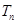 .
.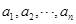 可以得到
可以得到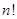 个不同的排列,每个排列为一行,写出一个
个不同的排列,每个排列为一行,写出一个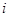 行
行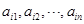 ,记
,记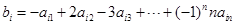 ,
,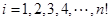 . 例如:用1,2,3,可得数阵如图所示,则
. 例如:用1,2,3,可得数阵如图所示,则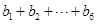 = ____ ;那么在用1,2,3,4,5形成的数阵中,
= ____ ;那么在用1,2,3,4,5形成的数阵中,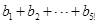 = .
= .
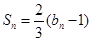 且
且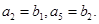
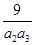 +
+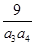 +
+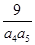 +…+
+…+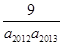 =( )
=( )




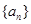 的前n项和为
的前n项和为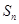 ,若
,若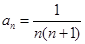 ,则
,则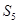 等于( )
等于( )