题目内容
12.设a,b是两条不同的直线,α,β是两不同的平面,则下列命题正确的是( )| A. | 若a∥α,b∥β,a∥b,则α∥β | B. | 若a∥b,a?α,b?β,则α∥β | ||
| C. | 若a∥α,b∥β,α∥β,则a∥b | D. | 若a⊥α,α∥β,b∥β,则a∥b |
分析 对四个选项,分别进行判断,即可得出正确答案.
解答 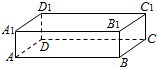 解:对于A,α∩β=c,当a,b都与c平行时,满足条件,故A不正确;
解:对于A,α∩β=c,当a,b都与c平行时,满足条件,故A不正确;
对于B,α∩β=c,当a,b都与c平行时,满足条件,故B不正确;
对于C,用长方体验证.如图,设A1B1为a,平面AC为α,BC为b,平面A1C1为β,显然有a∥α,b∥β,α∥β,但得不到a∥b,不正确;
对于D,a⊥α,α∥β,则a⊥β,因为b∥β,所以a∥b,正确.
故选:D.
点评 本题主要考查空间内两直线,直线与平面,平面与平面间的位置关系,综合性强,方法灵活,属中档题.

练习册系列答案
相关题目
17.设随机变量ξ~B(n,p),且E(ξ)=1.6,D(ξ)=1.28,则n,p的值依次为( )
| A. | 8,0.2 | B. | 4,0.4 | C. | 5,0.32 | D. | 7,0.45 |
4.已知x,y满足$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{x-y≤0}\end{array}\right.$,在(x-2)2+(y+1)2的最小值为( )
| A. | 5 | B. | $\frac{9}{2}$ | C. | $\frac{1}{12}$ | D. | 17 |
2.设集合M={x|-2<x<3},P={x|x≤-1},那么“x∈M或x∈P”是“x∈M∩P”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
