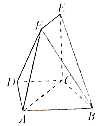题目内容
【题目】如图,在四棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,且
,且 ![]() ,
, ![]() 是
是 ![]() 的中点.
的中点.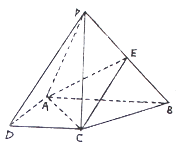
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的余弦值为
的余弦值为 ![]() ,求直线
,求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】
(1)解: ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
![]()
∴AC又 ![]() 平面
平面 ![]() ,
,
![]() 平面
平面 ![]() 平面
平面 ![]() 平面
平面 ![]() .
.
(2)解:如图,以C为原点, ![]() 为AB中点)、
为AB中点)、 ![]() 分别为x 轴、y 轴、Z 轴正向,建立空间直角坐标系,
分别为x 轴、y 轴、Z 轴正向,建立空间直角坐标系,
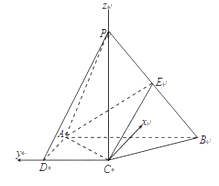
则 ![]() .
.
设 ![]() ,则
,则 ![]() ,
,
取 ![]() 为面
为面 ![]() 的法向量.
的法向量.
设 ![]() 为面
为面 ![]() 的法向量,则
的法向量,则 ![]() ,
,
即 ![]() 取
取 ![]() ,则
,则 ![]() ,则
,则 ![]() ,
,
依题意, 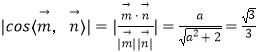 ,则
,则 ![]() .
.
于是 ![]() .
.
设直线 ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() ,
,
则 ![]() .
.
【解析】(1)由题意可先证出AC ⊥ PC ,AC ⊥BC即可得证A C ⊥ 平面 P B C进而得到平面 E A C ⊥ 平面 P B C。(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面 P A C和平面E A C的法向量,由向量垂直的坐标运算公式可求出法向量,再利用两个平面的夹角的余弦值可算a=1,于是得到面 E A C 的法向量进而可计算出直线与平面夹角的正弦值。
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直),还要掌握用空间向量求直线与平面的夹角(设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: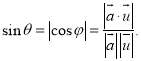 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

练习册系列答案
相关题目