题目内容
【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: ![]() ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记 ![]() ,求(t﹣1)(a+
,求(t﹣1)(a+ ![]() )的值.
)的值.
【答案】
(1)解:∵f(x)=ex+ax,∴f'(x)=ex+a,
若a≥0,则f'(x)>0,则函数f(x)在R上单调递增,这与题设矛盾.
∴a<0,
令f′(x)>0得x>ln(﹣a),令f′(x)<0得x<ln(﹣a),
∴f(x)在(﹣∞,ln(﹣a))上单调递减,在(ln(﹣a),+∞)上单调递增,
∴f(x)有两个零点,
∴fmin(x)=f(ln(﹣a))=﹣a+aln(﹣a),
∴﹣a+aln(﹣a)<0,解得a<﹣e.
(2)解:证明:∵x1,x2是f(x)的零点,∴ 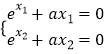 ,
,
两式相减得:a=﹣ ![]() .
.
记 ![]() =s,则f′(
=s,则f′( ![]() )=e
)=e ![]() ﹣
﹣ ![]() =
= ![]() [2s﹣(es﹣e﹣s)],
[2s﹣(es﹣e﹣s)],
设g(s)=2s﹣(es﹣e﹣s),则g′(s)=2﹣(es+e﹣s)<0,
∴g(s)是减函数,
∴g(s)<g(0)=0,
又 ![]() >0,∴f′(
>0,∴f′( ![]() )<0.
)<0.
∵f′(x)=ex+a是增函数,
∴f′( ![]() )<f′(
)<f′( ![]() )<0
)<0
(3)解:由 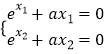 得
得 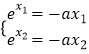 ,∴e
,∴e ![]() =﹣a
=﹣a ![]() ,
,
设P(x0,y0),在等边三角形ABC中,易知 ![]() ,y0=f(x0)<0,
,y0=f(x0)<0,
由等边三角形性质知y0=﹣ ![]() ,∴y0+
,∴y0+ ![]() =0,即
=0,即 ![]() ,
,
∴﹣a ![]() +
+ ![]() (x1+x2)+
(x1+x2)+ ![]() =0,
=0,
∵x1>0,∴  ,
,
∴﹣at+ ![]() (t2+1)+
(t2+1)+ ![]() (t2﹣1)=0,即(a+
(t2﹣1)=0,即(a+ ![]() )t2﹣2at+a﹣
)t2﹣2at+a﹣ ![]() =0,
=0,
∴[(a+ ![]() )t+
)t+ ![]() ](t﹣1)=0,
](t﹣1)=0,
∵t>1,∴(a+ ![]() )t+
)t+ ![]() =0,
=0,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)讨论a的符号,判断f(x)的单调性,计算f(x)的极值,根据零点个数得出f(x)的极小值为负数,列出不等式解出a;(2)计算f′( ![]() ),根据函数单调性判断f′(
),根据函数单调性判断f′( ![]() )的符号,根据f′(x)的单调性得出结论;(3)用x1 , x2表示出P点坐标,根据等边三角形的性质列方程化简即可求出t和a的关系,再计算(t﹣1)(a+
)的符号,根据f′(x)的单调性得出结论;(3)用x1 , x2表示出P点坐标,根据等边三角形的性质列方程化简即可求出t和a的关系,再计算(t﹣1)(a+ ![]() )的值.
)的值.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).