Question

【题目】选修4-4：坐标系与参数方程
将圆 （ 为参数）上的每一个点的横坐标保持不变，纵坐标变为原来的 ，得到曲线 ．
（1）求曲线 的普通方程；
（2）设 ， 是曲线 上的任意两点，且 ，求 的值．

Answer 1

【答案】
（1）解：设 为圆上的任意一点，在已知的变换下变为 上的点 ，

则有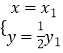

（2）解：以坐标原点 为极点， 轴正半轴为极轴，建立极坐标系，在极坐标系中，

曲线C化为极坐标方程得： ，设A ，B ，

则|OA|= ，|OB|= .则 = .

【解析】(1)利用极坐标和一般坐标的转化关系根据题意的伸缩变换，把函数关系进行转化得到直角坐标系下的椭圆的方程。(2)根据边的垂直关系，利用三角函数的恒等变换即可求得结果。