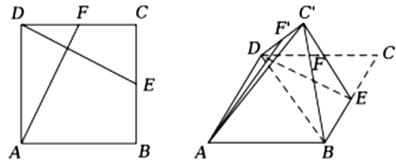
题目内容
【题目】△ABC中，角A，B，C的对边分别为a，b，c，且2bcosC+c=2a．
（Ⅰ）求角B的大小；
（Ⅱ）若
，求
的值．
【答案】（1）
（2）
【解析】试题分析：（1）由于2bcosC+c=2a，是关于边的一次齐次式，所以用正弦定理把边化为角，可得到
，
。（2）由（1）中和
，可知A，B角己知，同时根据三角形内角为
，也可以sinC,所以
，可解。
试题解析：（Ⅰ）在△ABC中，∵2bcosC+c=2a，
由正弦定理，得2sinBcosC+sinC=2sinA，
∵A+B+C=π，
∴sinA=sin（B+C）=sinBcosC+cosBsinC，…
∴2sinBcosC+sinC=2（sinBcosC+cosBsinC），
∴sinC=2cosBsinC，
∵0＜C＜π，∴sinC≠0，
∴，
∵0＜B＜π，∴．
（Ⅱ）∵三角形ABC中，
，
∴
，
∴
，
∴
练习册系列答案
相关题目
【题目】
是指大气中直径小于或等于
微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大.我国
标准采用世卫组织设定的最宽限值.即
日均值在35微克/立方米以下空气质量为一级；在35微克/立方米
75微克/立方米之间空气质量为二级；75微克/立方米以上空气质量为超标.
某市环保局从360天的市区
监测数据中统计了1月至10月的每月的平均值（单位：微克/立方米），如下表所示.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 32 | 28 | 25 | 31 | 34 | 33 | 45 | 44 | 63 | 68 |
（1）从5月到10月的这6个数据中任取2个数值，求这个2个数值均为二级的概率；
（2）求月均值
关于月份
的回归直线方程
，其中
.