题目内容
14.已知点P(x,y)的坐标满足条件$\left\{\begin{array}{l}{x+y≤4}\\{y≥x}\\{x≥1}\end{array}\right.$ 则x2+y2的最大值为10.分析 先画出满足约束条件件$\left\{\begin{array}{l}x+y≤4\\ y≥x\\ x≥1\end{array}\right.$的平面区域,z=x2+y2表示动点到原点的距离的平方,只需求出可行域内的动点到原点的距离最大值即可.
解答 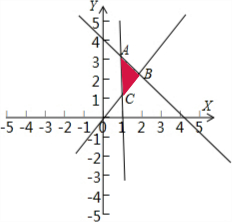 解:满足约束条件件 $\left\{\begin{array}{l}x+y≤4\\ y≥x\\ x≥1\end{array}\right.$的平面区域如下图所示:
解:满足约束条件件 $\left\{\begin{array}{l}x+y≤4\\ y≥x\\ x≥1\end{array}\right.$的平面区域如下图所示:
因为目标函数所表示的几何意义是动点到原点的距离的平方,
由图得当为A点时取得目标函数的最大值,
可知A点的坐标为(1,3),
代入目标函数中,可得zmax=32+12=10.
故答案为:10.
点评 本题考查的知识点是简单线性规划,其中画出满足约束条件的平面区域,找出目标函数的最优解点的坐标是解答本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.已知圆C1:x2+y2+2x+2y+1=0与圆C2:x2+y2-2x-2y+1=0关于直线l对称,则直线l的方程为( )
| A. | x+y=0 | B. | x+y+l=0 | C. | x=0 | D. | y=0 |
5.数列5,9,13,…的一个通项公式为( )
| A. | an=5+4n | B. | an=5-4n | C. | an=1+4n | D. | an=1-4n |
2.已知抛物线y=a(x-1)2+h(a≠0)与x轴交于A(x1,0)、B(4,0)两点,则x1为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.