题目内容
5．数列5，9，13，…的一个通项公式为（ ）| A． | an=5+4n | B． | an=5-4n | C． | an=1+4n | D． | an=1-4n |
分析 由数列的前几项判断数列是一个等差数列，进行求解即可．
解答 解：法1：∵9=5+4，13=9+4=5+2×4，
…
∴an=5+4（n-1）=1+4n，
法2：（公式法）∵9-5=4，13-9=4，
∴数列是一个以5为首项，4为公差的等差数列，则an=5+4（n-1）=1+4n，
故选：C
点评 本题主要考查数列通项公式的求解，比较基础．
练习册系列答案
相关题目
16．
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此做了4次试验，得到数据如下：
（Ⅰ）在给定的坐标系中画出表中数据的散点图；
（Ⅱ）求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅲ）试预测加工10个零件需要的时间．
参考公式：$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$．
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此做了4次试验，得到数据如下：| 零件的个数x（个） | 2 | 3 | 4 | 5 |
| 加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（Ⅱ）求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅲ）试预测加工10个零件需要的时间．
参考公式：$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$．
17．一梯形的直观图是一个如图所示的等腰梯形，且该梯形的面积为2，则原梯形的面积为（ ）
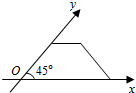
| A． | 2 | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |