题目内容
2．已知抛物线y=a（x-1）2+h（a≠0）与x轴交于A（x1，0）、B（4，0）两点，则x1为（ ）| A． | -2 | B． | -1 | C． | 0 | D． | 1 |
分析 根据抛物线的顶点式方程知对称轴x=1=$\frac{{x}_{1}+4}{2}$，据此可以求得x1的值．
解答 解：∵抛物线的解析式是：y=a（x-1）2+h（a≠0），
∴该抛物线的对称轴x=1．
又∵抛物线y=a（x-1）2+h（a≠0）与x轴交于A（x1，0）、B（4，0）两点，
∴1=$\frac{{x}_{1}+4}{2}$，
解得，x1=-2．
故选：A．
点评 本题考查了抛物线与x轴的交点．解答该题的技巧在于利用对称轴方程的定义和顶点式解析式的y=a（x-1）2+h（a≠0）的顶点（1，h）来求x1的值．
练习册系列答案
相关题目
17．一梯形的直观图是一个如图所示的等腰梯形，且该梯形的面积为2，则原梯形的面积为（ ）
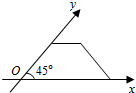
| A． | 2 | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
如图，直线AB过x轴上的点A（2，0），且与抛物线y=ax2相交于B、C两点，B点坐标为（1，1）．