题目内容
(本 题满分 13分)设函数
题满分 13分)设函数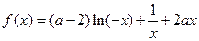 (
(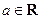 ).
).
(1)当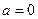 时,求
时,求 的极值;
的极值;
(2)当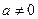 时,求
时,求 的单调区间.
的单调区间.
 题满分 13分)设函数
题满分 13分)设函数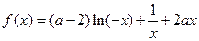 (
(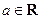 ).
).(1)当
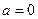 时,求
时,求 的极值;
的极值;(2)当
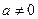 时,求
时,求 的单调区间.
的单调区间.(1) 取得极大值为
取得极大值为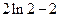 .
.
(2)当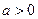 时,
时, 的增区间为
的增区间为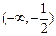 ,减区间为
,减区间为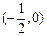 ;
;
当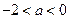 时,
时, 的增区间为
的增区间为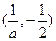 ,减区间为
,减区间为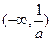 ,
,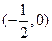 ;
;
当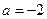 时,
时, 的减区间为
的减区间为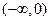 ,无增区间;
,无增区间;
当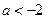 时,
时, 的增区间为
的增区间为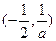 ,减区间为
,减区间为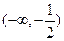 ,
,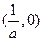 .
.
 取得极大值为
取得极大值为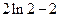 .
.(2)当
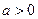 时,
时, 的增区间为
的增区间为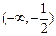 ,减区间为
,减区间为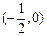 ;
;当
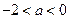 时,
时, 的增区间为
的增区间为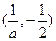 ,减区间为
,减区间为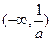 ,
,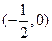 ;
;当
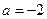 时,
时, 的减区间为
的减区间为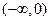 ,无增区间;
,无增区间;当
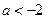 时,
时, 的增区间为
的增区间为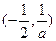 ,减区间为
,减区间为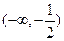 ,
,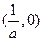 .
.(1)依题意,知 的定义域为
的定义域为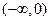 .
.
当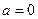 时,
时,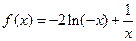 ,
,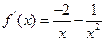
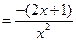 .
.
令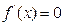 ,解得
,解得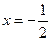 .
.
当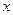 变化时,
变化时,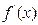 与
与 的变化情况如下表:
的变化情况如下表:
由上表知:当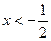 时,
时,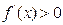 ;当
;当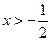 时,
时,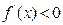 .
.
故当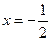 时,
时, 取得极大值为
取得极大值为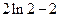 .
.
(2)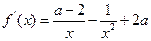
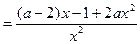
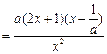
若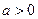 ,令
,令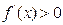 ,解得:
,解得: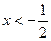 ;令
;令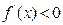 ,解得:
,解得: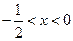 .
.
若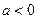 ,①当
,①当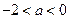 时,
时,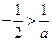
令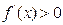 ,解得:
,解得: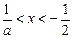 ;令
;令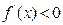 ,
,
解得: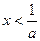 或
或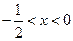 .
.
②当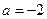 时,
时,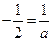 ,
,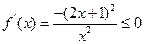
③当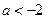 时,
时,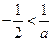 令
令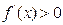 ,解得:
,解得: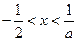 ;令
;令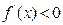 ,
,
解得: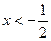 或
或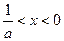 .
.
综上,当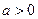 时,
时, 的增区间为
的增区间为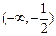 ,减区间为
,减区间为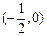 ;
;
当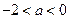 时,
时, 的增区间为
的增区间为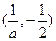 ,减区间为
,减区间为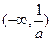 ,
,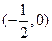 ;
;
当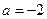 时,
时, 的减区间为
的减区间为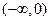 ,无增区间;
,无增区间;
当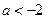 时,
时, 的增区间为
的增区间为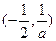 ,减区间为
,减区间为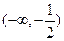 ,
,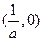 .
.
 的定义域为
的定义域为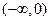 .
.当
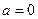 时,
时,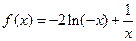 ,
,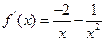
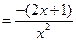 .
.令
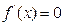 ,解得
,解得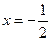 .
.当
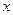 变化时,
变化时,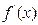 与
与 的变化情况如下表:
的变化情况如下表: | 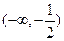 | 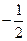 | 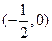 |
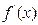 |  | 0 |  |
 | 单调递增 | 极大值 | 单调递减 |
由上表知:当
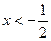 时,
时,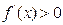 ;当
;当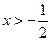 时,
时,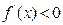 .
.故当
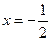 时,
时, 取得极大值为
取得极大值为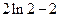 .
.(2)
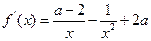
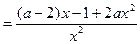
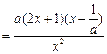
若
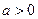 ,令
,令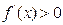 ,解得:
,解得: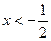 ;令
;令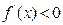 ,解得:
,解得: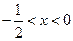 .
.若
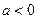 ,①当
,①当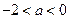 时,
时,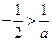
令
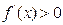 ,解得:
,解得: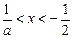 ;令
;令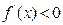 ,
,解得:
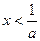 或
或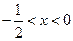 .
.②当
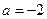 时,
时,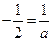 ,
,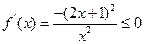
③当
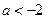 时,
时,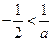 令
令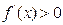 ,解得:
,解得: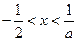 ;令
;令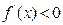 ,
,解得:
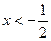 或
或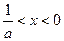 .
.综上,当
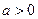 时,
时, 的增区间为
的增区间为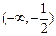 ,减区间为
,减区间为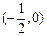 ;
;当
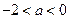 时,
时, 的增区间为
的增区间为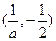 ,减区间为
,减区间为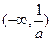 ,
,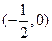 ;
;当
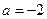 时,
时, 的减区间为
的减区间为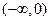 ,无增区间;
,无增区间;当
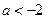 时,
时, 的增区间为
的增区间为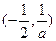 ,减区间为
,减区间为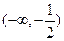 ,
,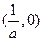 .
.
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
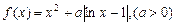
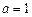 时,求
时,求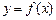 在
在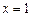 处的切线方程;
处的切线方程;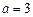 时,求
时,求 的极值;
的极值;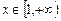 时,求
时,求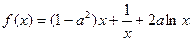 .
. 时,求
时,求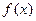 的最小值;
的最小值;  时,求
时,求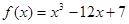 在
在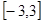 上的最大值与最小值的差是
上的最大值与最小值的差是



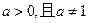 函数
函数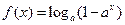 。
。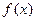 的定义域,并判断
的定义域,并判断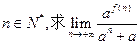 ;
;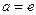 (
(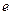 为自然对数的底数)时,设
为自然对数的底数)时,设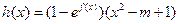 ,若函数
,若函数 的极值存在,求实数
的极值存在,求实数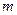 的取值范围以及函数
的取值范围以及函数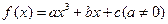 为奇函数,导函数
为奇函数,导函数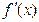 的最小值为-12,函数
的最小值为-12,函数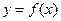 的图象在点P
的图象在点P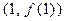 处的切线与直线
处的切线与直线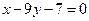 垂直.(1)求a,b,c的值;(2)求
垂直.(1)求a,b,c的值;(2)求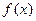 的各个单调区间,并求
的各个单调区间,并求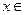 [-1, 3]时的最大值和最小值.
[-1, 3]时的最大值和最小值.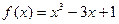 在闭区间
在闭区间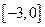 上的最大值,最小值分别是( )
上的最大值,最小值分别是( )
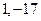
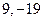

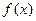 的定义域为区间
的定义域为区间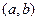 ,导函数
,导函数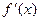 在
在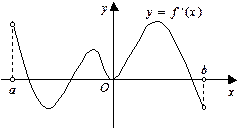
 个
个 个
个 个
个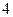 个[
个[