题目内容
(本小题满分12分)
已知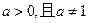 函数
函数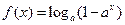 。
。
(Ⅰ)求函数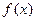 的定义域,并判断
的定义域,并判断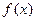 的单调性;
的单调性;
(Ⅱ)若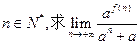 ;
;
(Ⅲ)当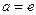 (
(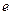 为自然对数的底数)时,设
为自然对数的底数)时,设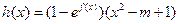 ,若函数
,若函数 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数 的极值。
的极值。
已知
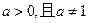 函数
函数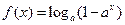 。
。(Ⅰ)求函数
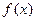 的定义域,并判断
的定义域,并判断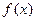 的单调性;
的单调性;(Ⅱ)若
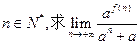 ;
;(Ⅲ)当
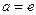 (
(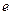 为自然对数的底数)时,设
为自然对数的底数)时,设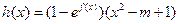 ,若函数
,若函数 的极值存在,求实数
的极值存在,求实数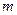 的取值范围以及函数
的取值范围以及函数 的极值。
的极值。(Ⅰ)
当
(Ⅱ)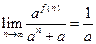
(Ⅲ)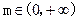 时,函数
时,函数 有极值;
有极值;
当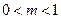 时
时 的极大值为
的极大值为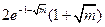 ,
, 的极小值为
的极小值为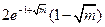
当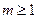 时,
时, 的极大值为
的极大值为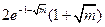
当

(Ⅱ)
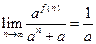
(Ⅲ)
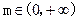 时,函数
时,函数 有极值;
有极值;当
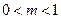 时
时 的极大值为
的极大值为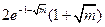 ,
, 的极小值为
的极小值为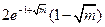
当
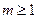 时,
时, 的极大值为
的极大值为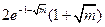
本小题主要考查函数、数列的极限、导数应用等基础知识、考查分类整合思想、推理和运算能力。
(Ⅰ)由题意知
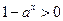
当
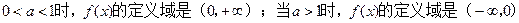
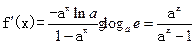
当
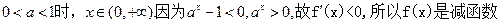
当
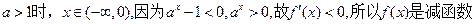 ….(4分)
….(4分)(Ⅱ)因为
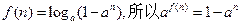
由函数定义域知
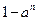 >0,因为n是正整数,故0<a<1.
>0,因为n是正整数,故0<a<1.所以
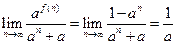
(Ⅲ)
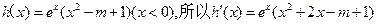
令
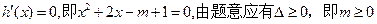
① 当m=0时,
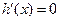 有实根
有实根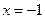 ,在
,在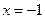 点左右两侧均有
点左右两侧均有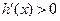 故无极值
故无极值② 当
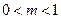 时,
时,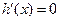 有两个实根
有两个实根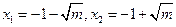
当x变化时,
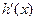 、
、 的变化情况如下表所示:
的变化情况如下表所示: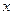 | 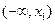 | 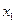 | 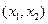 | 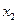 | 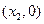 |
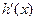 | + | 0 | - | 0 | + |
 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
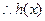 的极大值为
的极大值为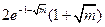 ,
, 的极小值为
的极小值为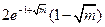
③ 当
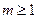 时,
时,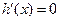 在定义域内有一个实根,
在定义域内有一个实根,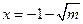
同上可得
 的极大值为
的极大值为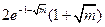
综上所述,
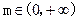 时,函数
时,函数 有极值;
有极值;当
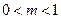 时
时 的极大值为
的极大值为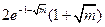 ,
, 的极小值为
的极小值为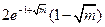
当
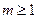 时,
时, 的极大值为
的极大值为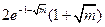

练习册系列答案
相关题目
 题满分 13分)设函数
题满分 13分)设函数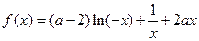 (
(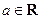 ).
).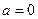 时,求
时,求 的极值;
的极值;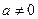 时,求
时,求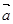 =(1,1),设f(x)=
=(1,1),设f(x)=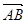 ·
·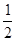 x
x ≤f(x
≤f(x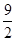 m-3都恒成立,求实数m的取值范围.
m-3都恒成立,求实数m的取值范围.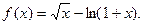
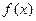 的定义域;
的定义域;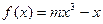 的图象上以N(1,n)为切点的切线倾斜角为
的图象上以N(1,n)为切点的切线倾斜角为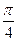 .
.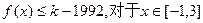 恒成立?若存在,求出最小的正整数k,否则请说明理由.
恒成立?若存在,求出最小的正整数k,否则请说明理由.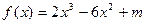 (m为常数)在
(m为常数)在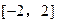 上有最大值3,那么此函数在
上有最大值3,那么此函数在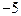
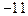
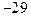
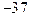
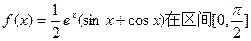 上的值域是 。
上的值域是 。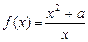 在
在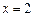 处取极值,则
处取极值,则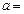 .
.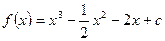 ,若对任意
,若对任意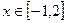 都有
都有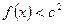 ,则
,则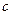 的取值范围是 .
的取值范围是 .