题目内容
4.若x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$,则z=x+y的最大值为$\frac{3}{2}$.分析 首先画出平面区域,然后将目标函数变形为直线的斜截式,求在y轴的截距最大值.
解答 解:不等式组表示的平面区域如图阴影部分,当直线经过D点时,z最大,
由$\left\{\begin{array}{l}{x-2y=0}\\{x+2y-2=0}\end{array}\right.$得D(1,$\frac{1}{2}$),
所以z=x+y的最大值为1+$\frac{1}{2}=\frac{3}{2}$;
故答案为:$\frac{3}{2}$.
点评 本题考查了简单线性规划;一般步骤是:①画出平面区域;②分析目标函数,确定求最值的条件.

练习册系列答案
相关题目
14.现有10张奖券,其中8张2元,2张5元,今某人随机无放回的抽取三张,则此人得奖金金额的数学期望为( )
| A. | 6元 | B. | 12元 | C. | 7.8元 | D. | 9元 |
19. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
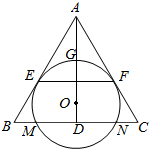 如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.