题目内容
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() , 底面
, 底面![]() 为梯形,
为梯形, ![]() ,
,![]() .
.
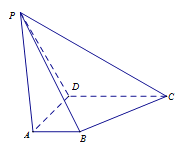
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行
都不平行
【答案】(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见证明
【解析】
(Ⅰ)利用线面平行判定定理即可证明AB∥平面PCD.
(Ⅱ)法一:利用面面垂直的性质即可证明AD⊥平面PCD.法二:在平面PCD中过点D作DH⊥CD,交PC于H,利用面面垂直的性质可证DH⊥平面ABCD,进而利用线面垂直的性质可证DH⊥AD,再根据线面垂直的判定定理即可证明AD⊥平面PCD.
(Ⅲ)法一:假设存在棱BC上点F,使得MF∥PC,连接AC,取其中点N,有MN∥PC,即可证明MF与MN重合,即MF就是MC,由MC与PC相交,矛盾,即可问题得证.法二:假设存在棱BC上点F,使得MF∥PC,显然F与点C不同,可得P,M,F,C四点在同一个平面α中,即B∈FCα,A∈PMα,α就是点A,B,C确定的平面ABCD,且P∈α,这与P﹣ABCD为四棱锥矛盾,即可得解假设错误,问题得证.
(Ⅰ)因为![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
(Ⅱ)法一:
因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
法二:
在平面![]() 中过点
中过点![]() 作
作![]() ,交
,交![]() 于
于![]()
因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以![]()
又![]() ,
,![]()
所以![]() 平面
平面![]()
(Ⅲ)法一:
假设存在棱![]() 上点
上点![]() ,使得
,使得![]()
连接![]() ,取其中点
,取其中点![]()
在![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]()
因为过直线外一点只有一条直线和已知直线平行,所以![]() 与
与![]() 重合
重合
所以点![]() 在线段
在线段![]() 上,所以
上,所以![]() 是
是![]() ,
,![]() 的交点
的交点![]()
即![]() 就是
就是![]()
而![]() 与
与![]() 相交,矛盾,所以假设错误,问题得证
相交,矛盾,所以假设错误,问题得证
法二:
假设存在棱![]() 上点
上点![]() ,使得
,使得![]() ,显然
,显然![]() 与点
与点![]() 不同
不同
所以![]() 四点在同一个平面
四点在同一个平面![]() 中
中
所以![]()
![]() ,
,![]()
![]()
所以![]()
![]() ,
,![]()
![]()
所以![]() 就是点
就是点![]() 确定的平面
确定的平面![]() ,且
,且![]()
![]()
这与![]() 为四棱锥矛盾,所以假设错误,问题得证
为四棱锥矛盾,所以假设错误,问题得证

【题目】《最强大脑》是江苏卫视引进德国节目《SuperBrain》而推出的大型科学竞技真人秀节目.节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关;
以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,然后再从这11名学生中抽取3名参加某期《最强大脑》,设抽到的3名学生中女生的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 | 频数 | 频率 |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
合计 | 50 | 1 |
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[6,6.5)的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.
【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
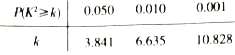 .
.