题目内容
(本小题满分12分)某工厂用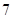 万元钱购买了一台新机器,运输安装费用
万元钱购买了一台新机器,运输安装费用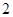 千元,每年投保、动力消耗的费用也为
千元,每年投保、动力消耗的费用也为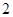 千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为
千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为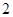 千元,第二年为
千元,第二年为 千元,第三年为
千元,第三年为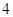 千元,依此类推,即每年增加
千元,依此类推,即每年增加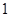 千元.
千元.
(Ⅰ)求使用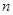 年后,保养、维修、更换易损零件的累计费用S(千元)关于
年后,保养、维修、更换易损零件的累计费用S(千元)关于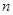 的表达式;
的表达式;
(Ⅱ)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数 )
(Ⅰ)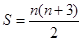 (Ⅱ)最佳年限是12年,平均费用为15.5千元
(Ⅱ)最佳年限是12年,平均费用为15.5千元
解析试题分析:(Ⅰ)由题易知其费用成等差数列, ……2分
所以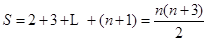 ……5分
……5分
(Ⅱ)设使用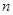 年的年平均费用为
年的年平均费用为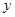 ,则
,则 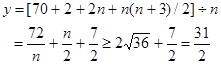 ……10分
……10分
当且仅当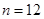 时,取等号,
时,取等号,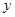 取最小值 , ……11分
取最小值 , ……11分
故最佳年限是12年,平均费用为15.5千元. ……12分
考点:本小题主要考查应用等差数列和基本不等式解决实际应用题,考查学生的理解能力和从实际问题中抽象出数学模型的能力.
点评:根据实际问题抽象出函数的解析式后,只需利用基本不等式就可求得函数的最值,但是一定要注意在定义域(使实际问题有意义的自变量的取值范围)内求解.

练习册系列答案
相关题目
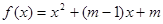 ,
,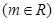
 是偶函数,求
是偶函数,求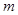 的值。
的值。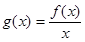 ,
,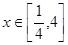 ,求
,求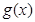 的最小值。
的最小值。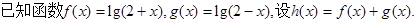
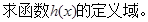
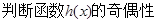 ,并说明理由.
,并说明理由.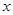 ,
,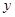 与x的函数解析式;
与x的函数解析式;
 的函数
的函数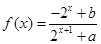 是奇函数.
是奇函数. 的值;
的值; ,不等式
,不等式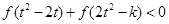 恒成立,求
恒成立,求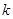 的取值范围.
的取值范围.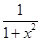 在(-∞,0)上的增减性.
在(-∞,0)上的增减性.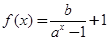
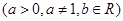 是奇函数,且
是奇函数,且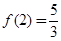
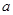 ,
,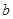 的值;
的值; 在区间
在区间 上是减函数.
上是减函数. 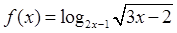
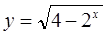 .
. .
.