题目内容
(本小题满分12分)
已知定义域为 的函数
的函数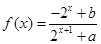 是奇函数.
是奇函数.
(1)求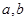 的值;
的值;
(2)若对任意的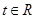 ,不等式
,不等式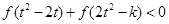 恒成立,求
恒成立,求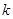 的取值范围.
的取值范围.
(1)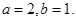 (2)
(2)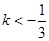
解析试题分析:(1)因为 是奇函数,所以
是奇函数,所以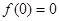 ,即
,即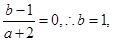
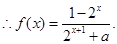 ……2分
……2分
又由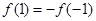 知
知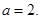
综上所述,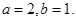 ……4分
……4分
(2)由(1)知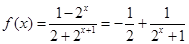 ,
,
易知 在
在 上为减函数. ……6分
上为减函数. ……6分
又因 是奇函数,从而有不等式:
是奇函数,从而有不等式: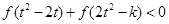
等价于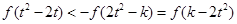 ,……8分
,……8分
因 为减函数,由上式推得:
为减函数,由上式推得: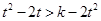 .
.
即对一切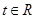 有:
有: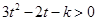 ,
,
从而判别式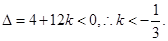 ……12分
……12分
考点:本小题考查函数的奇偶性、单调性及恒成立问题.
点评:函数的奇偶性、单调性及恒成立问题,都是高考中常考的内容.解决恒成立问题一般都转化成求最值来解决,而要求函数的最值,函数的单调性是高考中一定会考查的内容.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
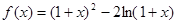 .
.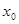 ,使不等式
,使不等式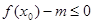 成立,求实数
成立,求实数 的最小值;
的最小值;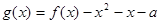 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 取值范围.
取值范围. (
(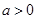 ),
),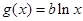 .
.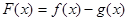 ,讨论
,讨论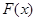 的单调性;
的单调性; 的不等式
的不等式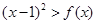 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数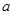 的取值范围;
的取值范围; 与
与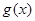 定义域上的任意实数
定义域上的任意实数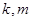 ,使得
,使得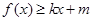 和
和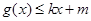 都成立,则称直线
都成立,则称直线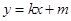 为函数
为函数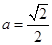 ,
,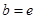 ,试探究
,试探究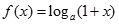 ,
,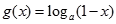 ,
,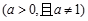 .
.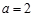 ,函数
,函数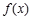 的定义域为
的定义域为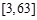 ,求函数
,求函数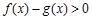 的
的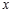 的取值范围.
的取值范围.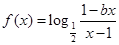 为奇函数,
为奇函数,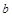 为常数.
为常数.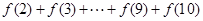 的值;
的值;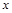 的值,不等式
的值,不等式 >
>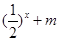 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.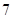 万元钱购买了一台新机器,运输安装费用
万元钱购买了一台新机器,运输安装费用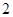 千元,每年投保、动力消耗的费用也为
千元,每年投保、动力消耗的费用也为 千元,第三年为
千元,第三年为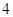 千元,依此类推,即每年增加
千元,依此类推,即每年增加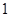 千元.
千元.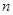 年后,保养、维修、更换易损零件的累计费用S(千元)关于
年后,保养、维修、更换易损零件的累计费用S(千元)关于 为定义在
为定义在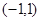 上的奇函数,当
上的奇函数,当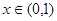 时,
时,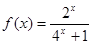 ;
;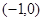 上的单调性,并给出证明.
上的单调性,并给出证明.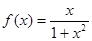 .
.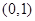 上的单调性并证明;
上的单调性并证明;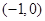 上的增减性.(不用证明)
上的增减性.(不用证明)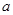 为实数,函数
为实数,函数 。
。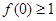 ,求
,求 的最小值
的最小值 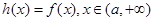 ,直接写出(不需要给出演算步骤)不等式
,直接写出(不需要给出演算步骤)不等式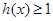 的解集。
的解集。