题目内容
19.设a>b>0,当a2+$\frac{4}{b(a-b)}$取得最小值时,函数f(x)=$\frac{a}{si{n}^{2}x}$+bsin2x的最小值为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
分析 根据基本不等求出a,b的值,再利用换元法,求出f(t)的最小值即可.
解答 解:a2+$\frac{4}{b(a-b)}$=a2+b2-ab+b(a-b)+$\frac{4}{b(a-b)}$≥2ab-ab+2$\sqrt{b(a-b)•\frac{4}{b(a-b)}}$=ab+4,
∴f(x)=$\frac{a}{si{n}^{2}x}$+bsin2x≥2$\sqrt{ab}$,
∵b(a-b)≤$\frac{(b+a-b)^{2}}{4}$=$\frac{{a}^{2}}{4}$,当且仅当a=2b时取等号,
∴a2+$\frac{4}{b(a-b)}$≥a2+$\frac{16}{{a}^{2}}$≥2$\sqrt{16}$=8,当且仅当a2=4时,即a=2时取等号,此时b=1,
∴f(x)=$\frac{a}{si{n}^{2}x}$+bsin2x=$\frac{2}{si{n}^{2}x}$+sin2x,
设sin2x=t,则t∈(0,1],
∴y=$\frac{2}{t}$+t,
∴y=$\frac{2}{t}$+t在(0,1]上单调递减,
∴ymin=$\frac{2}{1}$+1=3,
故选:A.
点评 本题考查了基本不等式的应用和函数的单调性和最值的关系,属于中档题.

练习册系列答案
相关题目
10.圆(x-4)2+y2=9和圆x2+(y-3)2=4的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
9.已知$\overrightarrow{a}$=(-2,0,1),$\overrightarrow{b}$=(2,k,3),$\overrightarrow{c}$=(1,-1,2),若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$三个向量共面,则实数k的值为( )
| A. | -$\frac{8}{5}$ | B. | -$\frac{1}{5}$ | C. | 1 | D. | $\frac{8}{5}$ |
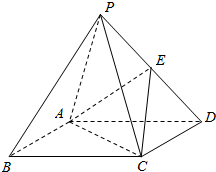 如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.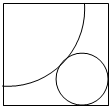 如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.