题目内容
在四边形ABCD中，∠A＝135°，∠B＝∠D＝90°，BC＝2，AD＝2，则四边形ABCD的面积是______．
4
因∠B＝∠D＝90°，于是设想构造直角三角形，延长BA与CD的延长线交于E，
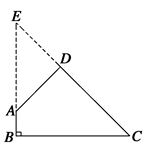
则得到Rt△BCE和Rt△ADE，由题目条件知，△ADE为等腰直角三角形，所以DE＝AD＝2，所以S△ADE＝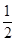
×2×2＝2.
又可证Rt△EBC∽Rt△EDA，
所以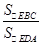
＝
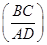2＝
2＝3.
∴S△EBC＝3S△EDA，∴S四边形ABCD＝S△EBC－S△ADE＝4.
则得到Rt△BCE和Rt△ADE，由题目条件知，△ADE为等腰直角三角形，所以DE＝AD＝2，所以S△ADE＝
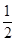×2×2＝2.又可证Rt△EBC∽Rt△EDA，
所以
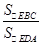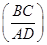＝2＝2＝3.∴S△EBC＝3S△EDA，∴S四边形ABCD＝S△EBC－S△ADE＝4.
练习册系列答案
相关题目
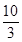，连接DE交BC于点F，AC＝4，BC＝3.求证：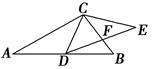
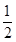BC，则sin∠MCA＝
＝
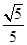
，AE＝BE，则有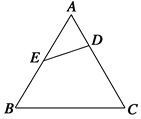
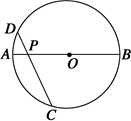
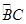上的点，若∠BAC＝80°，那么∠BDC＝________.
