题目内容
如图,AB为⊙O直径,MN切⊙O于C,AC=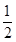 BC,则sin∠MCA=
BC,则sin∠MCA=

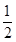 BC,则sin∠MCA=
BC,则sin∠MCA=
A.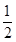 | B. |
C. | D.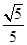 |
D
连接OC,

∵MN切⊙O于C,
∴OC⊥MN,
∴∠MCA+∠ACO=90°,
∵OC=OA,
∴∠ACO=∠CAO,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠CAO+∠B=90°,∴∠MCA=∠B,
∵AC=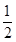 BC,即BC=2AC,
BC,即BC=2AC,
∴AB= =
=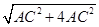 =
= AC,
AC,
∴sin∠B= =
= =
=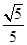 ,∴sin∠MCA=
,∴sin∠MCA=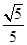 .
.

∵MN切⊙O于C,
∴OC⊥MN,
∴∠MCA+∠ACO=90°,
∵OC=OA,
∴∠ACO=∠CAO,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠CAO+∠B=90°,∴∠MCA=∠B,
∵AC=
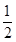 BC,即BC=2AC,
BC,即BC=2AC,∴AB=
 =
=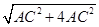 =
= AC,
AC,∴sin∠B=
 =
= =
=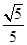 ,∴sin∠MCA=
,∴sin∠MCA=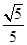 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 点在圆
点在圆 直径
直径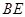 的延长线上,
的延长线上, 切圆
切圆 点,
点, 是
是 的平分线交
的平分线交 于点
于点 ,交
,交 于
于 点.
点.
 的度数;(2)若
的度数;(2)若 ,求
,求 .
. BC,CE=
BC,CE=
 ,点E,F分别为线段AB,AD的中点,则EF=________.
,点E,F分别为线段AB,AD的中点,则EF=________.





 的半径为
的半径为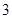 ,从圆
,从圆 引切线
引切线 和割线
和割线 ,圆心
,圆心 的距离为
的距离为 ,
, ,则切线
,则切线
