题目内容
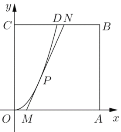
【题目】对任意正整数![]() ,若存在数列
,若存在数列![]() ,满足
,满足![]() ,其中
,其中![]() ,则称数列
,则称数列![]() 为正整数
为正整数![]() 的生成数列,记为
的生成数列,记为![]() .
.
(1)写出2018的生成数列![]() ;
;
(2)求证:对任意正整数![]() ,存在唯一的生成数列
,存在唯一的生成数列![]() ;
;
(3)求生成数列![]() 的所有项的和.
的所有项的和.
【答案】(1)数列![]() 为
为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据![]() 得到答案.
得到答案.
(2)只需证明两个不同的![]() 项生成数列表示的正整数不同,类推可得
项生成数列表示的正整数不同,类推可得![]() 的充要条件是生成数列
的充要条件是生成数列![]() 和
和![]() 相同,得到证明
相同,得到证明
(3)根据![]() 得到通项
得到通项
![]() ,计算得到答案.
,计算得到答案.
(1)![]() ,
,
所以数列![]() 为
为![]() ;
;
(2)对于恰有![]() 项的生成数列,其表示的正整数最小值为
项的生成数列,其表示的正整数最小值为![]() ,
,
表示的正整数最大值为![]()
即![]() 项的不同生成数列共有
项的不同生成数列共有![]()
而满足![]() 的正整数
的正整数![]() 恰好有
恰好有![]() 个
个
下面只需证明两个不同的![]() 项生成数列表示的正整数不同,
项生成数列表示的正整数不同,
设生成数列![]() 和
和![]() 表示的数为A和B,若
表示的数为A和B,若![]() ,
,![]()
即![]() ,同理,若有
,同理,若有![]() ,也可得
,也可得![]() .
.
依次类推可得![]() 的充要条件是生成数列
的充要条件是生成数列![]() 和
和![]() 相同.
相同.
综上可得,对任意正整数![]() ,存在唯一的生成数列
,存在唯一的生成数列![]() .
.
(3)因为![]()
所以![]()
即![]() 的通项为
的通项为![]()
故所有项的和为![]() .
.

练习册系列答案
相关题目
【题目】网购是现在比较流行的一种购物方式,现随机调查50名个人收入不同的消费者是否喜欢网购,调查结果表明:在喜欢网购的25人中有18人是低收入的人,另外7人是高收入的人,在不喜欢网购的25人中有6人是低收入的人,另外19人是高收入的人.
喜欢网购 | 不喜欢网购 | 总计 | |
低收入的人 | |||
高收入的人 | |||
总计 |
(Ⅰ)试根据以上数据完成![]() 列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
(Ⅱ)将5名喜欢网购的消费者编号为1、2、3、4、5,将5名不喜欢网购的消费者编号也记作1、2、3、4、5,从这两组人中各任选一人进行交流,求被选出的2人的编号之和为2的倍数的概率.
参考公式:
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |