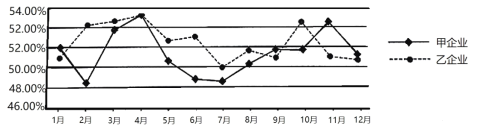
МвДїДЪИЭ
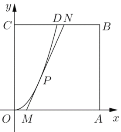
ЎѕМвДїЎїДіµШТЄЅЁФмТ»ёц±Яі¤ОЄ2ЈЁµҐО»Јє![]() Ј©µДХэ·ЅРОКРГсРЭПР№«Ф°
Ј©µДХэ·ЅРОКРГсРЭПР№«Ф°![]() Ј¬Ѕ«ЖдЦРµДЗшУт
Ј¬Ѕ«ЖдЦРµДЗшУт![]() їЄНЪіЙТ»ёціШМБЈ¬ИзНјЅЁБўЖЅГжЦ±ЅЗЧш±кПµєуЈ¬µг
їЄНЪіЙТ»ёціШМБЈ¬ИзНјЅЁБўЖЅГжЦ±ЅЗЧш±кПµєуЈ¬µг![]() µДЧш±кОЄ
µДЧш±кОЄ![]() Ј¬ЗъПЯ
Ј¬ЗъПЯ![]() КЗєЇКэ
КЗєЇКэ![]() НјПсµДТ»Ії·ЦЈ¬№э±Я
НјПсµДТ»Ії·ЦЈ¬№э±Я![]() ЙПТ»µг
ЙПТ»µг![]() ФЪЗшУт
ФЪЗшУт![]() ДЪЧчТ»ґОєЇКэ
ДЪЧчТ»ґОєЇКэ![]() ЈЁ
ЈЁ![]() Ј©µДНјПсЈ¬УлПЯ¶О
Ј©µДНјПсЈ¬УлПЯ¶О![]() Ѕ»УЪµг
Ѕ»УЪµг![]() ЈЁµг
ЈЁµг![]() І»Улµг
І»Улµг![]() ЦШєПЈ©Ј¬ЗТПЯ¶О
ЦШєПЈ©Ј¬ЗТПЯ¶О![]() УлЗъПЯ
УлЗъПЯ![]() УРЗТЦ»УРТ»ёц№«№Іµг
УРЗТЦ»УРТ»ёц№«№Іµг![]() Ј¬ЛД±ЯРО
Ј¬ЛД±ЯРО![]() ОЄВМ»Ї·зѕ°Зш.
ОЄВМ»Ї·зѕ°Зш.
ЈЁ1Ј©ЗуЦ¤Јє![]() Ј»
Ј»
ЈЁ2Ј©Йиµг![]() µДєбЧш±кОЄ
µДєбЧш±кОЄ![]() Ј¬
Ј¬
ўЩУГ![]() ±нКѕ
±нКѕ![]() Ўў
Ўў![]() БЅµгµДЧш±кЈ»
БЅµгµДЧш±кЈ»
ўЪЅ«ЛД±ЯРО![]() µДГж»э
µДГж»э![]() ±нКѕіЙ№ШУЪ
±нКѕіЙ№ШУЪ![]() µДєЇКэ
µДєЇКэ![]() Ј¬ІўЗу
Ј¬ІўЗу![]() µДЧоґуЦµ.
µДЧоґуЦµ.
Ўѕґр°ёЎїЈЁ1Ј©јыЅвОцЈЁ2Ј©ўЩMЈЁ![]() Ј¬0Ј©Ј¬NЈЁ
Ј¬0Ј©Ј¬NЈЁ![]() Ј¬2Ј©ўЪSЈЅ4©ЃЈЁt
Ј¬2Ј©ўЪSЈЅ4©ЃЈЁt![]() Ј©Ј¬ЖдЦР0ЈјtЈј1Ј¬SµДЧоґуЦµКЗ4
Ј©Ј¬ЖдЦР0ЈјtЈј1Ј¬SµДЧоґуЦµКЗ4![]() Ј®
Ј®
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭєЇКэyЈЅax2№эµгDЈ¬ЗуіцЅвОцКЅyЈЅ2x2Ј»
УЙ![]() ПыИҐyЈ¬АыУГЎчЈЅ0Ц¤ГчЅбВЫіЙБўЈ»
ПыИҐyЈ¬АыУГЎчЈЅ0Ц¤ГчЅбВЫіЙБўЈ»
ЈЁ2Ј©ўЩРґіцµгPµДЧш±кЈЁtЈ¬2t2Ј©Ј¬ґъИлЦ±ПЯMNµД·ЅіМЈ¬УГt±нКѕіцЦ±ПЯ·ЅіМЈ¬
АыУГЦ±ПЯ·ЅіМЗуіцMЎўNµДЧш±кЈ»
ўЪЅ«ЛД±ЯРОMABNµДГж»эS±нКѕіЙ№ШУЪtµДєЇКэSЈЁtЈ©Ј¬
АыУГ»щ±ѕІ»µИКЅјґїЙЗуіцSµДЧоґуЦµЈ®
ЈЁ1Ј©єЇКэyЈЅax2№эµгDЈЁ1Ј¬2Ј©Ј¬
ґъИлјЖЛгµГaЈЅ2Ј¬
ЎаyЈЅ2x2Ј»
УЙ![]() Ј¬ПыИҐyµГ2x2©Ѓkx©ЃbЈЅ0Ј¬
Ј¬ПыИҐyµГ2x2©Ѓkx©ЃbЈЅ0Ј¬
УЙПЯ¶ОMNУлЗъПЯODУРЗТЦ»УРТ»ёц№«№ІµгPЈ¬
µГЎчЈЅЈЁ©ЃkЈ©2©Ѓ4ЎБ2ЎБbЈЅ0Ј¬
ЅвµГb![]() Ј»
Ј»
ЈЁ2Ј©ЙиµгPµДєбЧш±кОЄtЈ¬Фт0ЈјtЈј1Ј¬
ЎаµгPЈЁtЈ¬2t2Ј©Ј»
ўЩЦ±ПЯMNµД·ЅіМОЄyЈЅkx+bЈ¬
јґyЈЅkx![]() №эµгPЈ¬
№эµгPЈ¬
Ўаkt![]() 2t2Ј¬
2t2Ј¬
ЅвµГkЈЅ4tЈ»
yЈЅ4tx©Ѓ2t2
БоyЈЅ0Ј¬ЅвµГx![]() Ј¬ЎаMЈЁ
Ј¬ЎаMЈЁ![]() Ј¬0Ј©Ј»
Ј¬0Ј©Ј»
БоyЈЅ2Ј¬ЅвµГx![]() Ј¬ЎаNЈЁ
Ј¬ЎаNЈЁ![]() Ј¬2Ј©Ј»
Ј¬2Ј©Ј»
ўЪЅ«ЛД±ЯРОMABNµДГж»эS±нКѕіЙ№ШУЪtµДєЇКэОЄ
SЈЅSЈЁtЈ©ЈЅ2ЎБ2![]() 2ЎБ[
2ЎБ[![]() ЈЁ
ЈЁ![]() Ј©]ЈЅ4©ЃЈЁt
Ј©]ЈЅ4©ЃЈЁt![]() Ј©Ј¬ЖдЦР0ЈјtЈј1Ј»
Ј©Ј¬ЖдЦР0ЈјtЈј1Ј»
УЙt![]() 2
2![]() Ј¬µ±ЗТЅцµ±t
Ј¬µ±ЗТЅцµ±t![]() Ј¬јґt
Ј¬јґt![]() К±Ў°ЈЅЎ±іЙБўЈ¬
К±Ў°ЈЅЎ±іЙБўЈ¬
ЛщТФSЎЬ4![]() Ј»јґSµДЧоґуЦµКЗ4
Ј»јґSµДЧоґуЦµКЗ4![]() Ј®
Ј®