题目内容
函数y=3x2+
的最小值是( )
| 6 |
| x2+1 |
A.3
| B.-3 | C.6
| D.6
|
令t=x2+1(t≥1),
则y=3(t-1)+
=3t+
-3≥2
-3=6
-3,
当且仅当3t=
,
即t=
时,函数y=3x2+
的最小值是6
-3.
故选D.
则y=3(t-1)+
| 6 |
| t |
| 6 |
| t |
3t•
|
| 2 |
当且仅当3t=
| 6 |
| t |
即t=
| 2 |
| 6 |
| x2+1 |
| 2 |
故选D.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
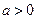 且
且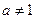 时,函数
时,函数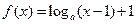 的图像恒过点
的图像恒过点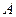 ,若点
,若点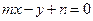 上,则
上,则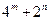 的最小值为
的最小值为 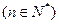 .
.