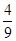题目内容

在某两个正数x，y之间，若插入一个正数a，使x，a，y成等比数列；若插入两个正数b，c，使x，b，c，y成等差数列，求证：（a+1）2≤（b+1）（c+1）．
∵x，a，y成等比数列
∴a2=xy
∵a＞1
∴a=
xy

∵x，b，c，y成等差数列
∴b-x=c-b=y-c
即b=
2x+y
3
，c=
x+2y
3

∴（b+1）（c+1）=(
2x+y
3
+1)（
x+2y
3
+1）=
2(x2+y2)+5xy+9x+9y+9
9

∵x＞0，y＞0
∴
2(x2+y2)+5xy+9x+9y+9
9
≥
2×(2xy)+5xy
9
+2
xy
+1=(
xy
+1)2=（a+1）2
即：（a+1）2≤（b+1）（c+1）．
练习册系列答案
相关题目
函数y=3x2+
6
x2+1
的最小值是（　　）
A．3
2
-3		B．-3C．6
2
D．6
2
-3
已知实数x，y满足：x2+y2=1，则x+y的取值范围是（　　）
A．[-
2
，
2
]		B．[-1，1]C．[1，
2
]		D．(1，
2
]
已知等比数列{an}中，公比q＞0，若a2=3，则a1+a2+a3的最值情况为（　　）
A．有最小值3B．有最大值12C．有最大值9D．有最小值9
设函数f（x）=2x+
1
x
-1（x＜0），则f（x）（　　）
A．有最大值B．有最小值C．是增函数D．是减函数
已知x＞0，y＞0，且x+y=1，则
1
x
+
1
y
的最小值为（　　）
A．1B．2C．3D．4
已知x，y都是正数
（1）若3x+2y=12，求xy的最大值；
（2）若
4
x
+
16
y
=1，求x+y的最小值．
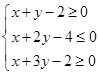不等式组表示的平面区域的面积为________．
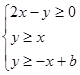实数x，y满足，则的最小值为3，则实数b的值为（   ）  
A．B．—C．D．—

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网