题目内容
【题目】一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为![]() .记方法二抽取的不合格产品数为
.记方法二抽取的不合格产品数为![]() .
.
(1)求两种抽取方式下![]() ,
,![]() 的概率分布列;
的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
【答案】(1)![]() ,
,![]() 的分布列见解析;(2)平均数相等,理由见解析.
的分布列见解析;(2)平均数相等,理由见解析.
【解析】
(1)![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从超几何分布,计算对应的概率,列出频率分布列;
服从超几何分布,计算对应的概率,列出频率分布列;![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从二项分布,计算对应的概率,列出频率分布列;
服从二项分布,计算对应的概率,列出频率分布列;
(2)分别计算方法一与方法二中的平均数(期望),比较结果即可.
(1)方法一中随机变量![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从超几何分布,
服从超几何分布,
于是![]() ;
;![]() ;
;
![]() ;
;
因此![]() 的频率分布可表示为下表:
的频率分布可表示为下表:
| 0 | 1 | 2 |
|
|
|
|
方法二中随机变量![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从二项分布,
服从二项分布,
于是![]() ;
;![]() ;
;
![]() ;
;
因此![]() 的频率分布可表示为下表:
的频率分布可表示为下表:
| 0 | 1 | 2 |
|
|
|
|
(2)由(1)知,方法一中![]() 的数学期望为
的数学期望为![]() ,
,
方法二中![]() 的数学期望为
的数学期望为![]() ,
,
所以两种方式抽到的不合格品平均数相等.

【题目】某研究机构为了了解大学生对冰壶运动的兴趣,随机从某校学生中抽取了100人进行调查,经统计男生与女生的人数比为![]() ,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
(1)完成![]() 列联表,并判断能否有
列联表,并判断能否有![]() 把握认为“对冰壶运动是否有兴趣与性别有关”?
把握认为“对冰壶运动是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 20 | ||
女 | 15 | ||
合计 | 100 |
(2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取6人,求抽取的男生和女生分别为多少人?若从这6人中选取两人作为冰壶运动的宣传员,求选取的2人中恰好有1位男生和1位女生的概率.
附:参考公式1.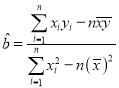 ,
,![]() );2.
);2.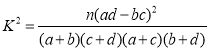 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |