题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)若对![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;②当
上单调递增;②当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
(2)![]() .
.
【解析】
(1)求出函数的定义域和导函数, ![]() ,对
,对![]() 讨论,得导函数的正负,得原函数的单调性;(2)法一: 由
讨论,得导函数的正负,得原函数的单调性;(2)法一: 由![]() 得
得![]() ,
,
分别运用导函数得出函数![]() (
(![]() ),
),![]() 的单调性,和其函数的最值,可得
的单调性,和其函数的最值,可得![]() ,可得的范围;
,可得的范围;
法二:由![]() 得
得![]() ,化为
,化为![]() 令
令![]() (
(![]() ),研究函数的单调性,可得
),研究函数的单调性,可得![]() 的取值范围.
的取值范围.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 得
得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
(2)法一: 由![]() 得
得![]() ,
,
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
令![]() ,
,
则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,
,
![]() (*)
(*)
当![]() 时,
时,![]() ,
,![]() (*)式恒成立,即
(*)式恒成立,即![]() 恒成立,满足题意
恒成立,满足题意
法二:由![]() 得
得![]() ,
,![]() ,
,![]()
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递增,
上单调递增,![]() 恒成立,满足题意
恒成立,满足题意
当![]() 时,令
时,令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,使得
,使得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() ,不满足题意,
,不满足题意,
综上所述,![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
【题目】为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级100名学生进行不记名问卷调查,得到如下数据:
近视 | 不近视 | |
足够的户外暴露时间 | 20 | 35 |
不足够的户外暴露时间 | 30 | 15 |
(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否认为在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
附: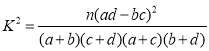 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |