题目内容
【题目】已知函数![]() .
.
(1)若函数![]() ,试讨论
,试讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)由于函数![]() ,得出
,得出![]() ,分类讨论当
,分类讨论当![]() 和
和![]() 时,
时,![]() 的正负,进而得出
的正负,进而得出![]() 的单调性;
的单调性;
(2)求出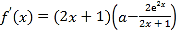 ,令
,令![]() ,得
,得![]() ,设
,设![]() ,通过导函数
,通过导函数![]() ,可得出
,可得出![]() 在
在![]() 上的单调性和值域,再分类讨论
上的单调性和值域,再分类讨论![]() 和
和![]() 时,
时,![]() 的单调性,再结合
的单调性,再结合![]() ,
,![]() 恒成立,即可求出
恒成立,即可求出![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,
,
所以![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
②当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)因为![]() ,可知
,可知![]() ,
,
![]()
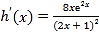 ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在
在![]() 上的值域是
上的值域是![]() ,即
,即![]() .
.
当![]() 时,
时,![]() 没有实根,且
没有实根,且![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,符合题意.
,符合题意.
当![]() 时,
时,![]() ,
,
所以![]() 有唯一实根
有唯一实根![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,不符合题意.
,不符合题意.
综上,![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: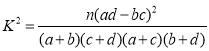 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |