题目内容
【题目】已知函数
，
.
（1）若函数
恰有两个不相同的零点，求实数
的值；
（2）记
为函数的所有零点之和，当
时，求的取值范围.
【答案】（1）
（2）
【解析】
分析：（1）在同一个坐标系中画出函数
的图像以及直线
，利用其交点个数，得到实数
的取值；
（2）随着参数a的取值变化，零点的情况也发生变化，分类讨论求得结果.
详解：（1）由
得
，函数
有两不同的零点等价于函数
的图像与直线有两不同的交点，在同一坐标系中，作函数和直线的图像。
如图所示：
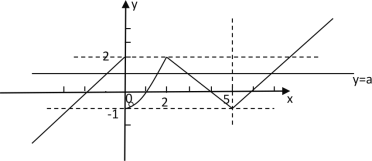由图可知，当且仅当
时，直线与函数的图像有两不同的交点，
即函数 有两不同的零点，
实数
（另解：可分段讨论得出实数的值）
（2）当
时，由（1）图可知，函数有四个不等的零点，从小到大依次设为
，则
，
，
时， 
的图像关于直线
对称，
，
，当时，函数
为增函数.
, 的取值范围是
练习册系列答案
阅读快车系列答案
相关题目
