题目内容
【题目】已知椭圆E： 
（a＞b＞0）的离心率为 
，其长轴长与短轴长的和等于6．
（1）求椭圆E的方程；
（2）如图，设椭圆E的上、下顶点分别为A1、A2 ， P是椭圆上异于A1、A2的任意一点，直线PA1、PA2分别交x轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值．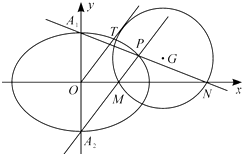 
【答案】
（1）解：由题意可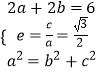得 
，解得 
．
∴椭圆E的方程为 
（2）解：由（1）可知：A1（0，1），A2（0，﹣1），设P（x0，y0），则 
．
则直线PA1的方程为 
，令y=0，得xN= 
；
直线PA2的方程为 
，令y=0，得 
．
由切割线定理可得：|OT|2=|OM||ON|= 
= 
=4，
∴|OT|=2，即线段OT的长为定值2
【解析】（1）利用椭圆的标准方程及其性质即可得出；（2）利用直线的方程、点在椭圆上满足的条件、切割线定理即可得出．
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
