题目内容
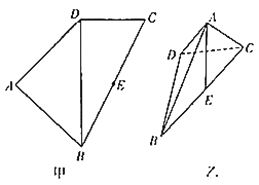
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为 ![]() .
. 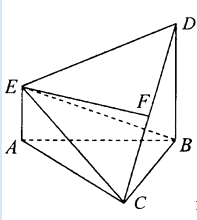
(1)若F是线段CD的中点,证明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
【答案】
(1)证明:取BC的中点为M,连接FM,则可证AM⊥平面BCD,四边形AEFM为平行四边形,
所以EF∥AM,所以EF⊥平面DBC
(2)解:取AB的中点O,连结OC,OD,则OC⊥平面ABD,∠CDO即是CD与平面ABDE所成角, ![]() ,
,
设AB=x,则有 ![]() ,得AB=2,取DE的中点为G,
,得AB=2,取DE的中点为G,
以O为原点,OC为x轴,OB为y轴,OG为z轴,建立如图空间直角坐标系,则 ![]() ,
,
由(1)知:BF⊥平面DEC,又取平面DEC的一个法向量 ![]() =(
=( ![]() ,﹣1,2),
,﹣1,2),
设平面BCE的一个法向量 ![]() =(1,y,z),由,由此得平面BCE的一个法向量
=(1,y,z),由,由此得平面BCE的一个法向量 ![]() =(1,
=(1, ![]() ,2
,2 ![]() ),
),
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() =
= ![]()
所以二面角D﹣EC﹣B的平面角的余弦值为 ![]()
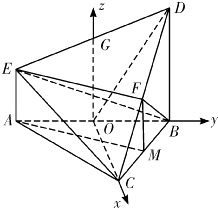
【解析】(1)根据线面垂直的判定定理进行证明即可.(2)建立坐标系,求出平面的法向量,利用向量法进行求解即可.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目