Question

【题目】给出下列命题：
（1）设f（x）与g（x）是定义在R上的两个函数，若|f（x1）+f（x2）|≥|g（x1）+g（x2）|恒成立，且f（x）为奇函数，则g（x）也是奇函数；
（2）若x1 ， x2∈R，都有|f（x1）﹣f（x2）|＞|g（x1）﹣g（x2）|成立，且函数f（x）在R上递增，则f（x）+g（x）在R上也递增；
（3）已知a＞0，a≠1，函数f（x）= ，若函数f（x）在[0，2]上的最大值比最小值多 ，则实数a的取值集合为 ；
（4）存在不同的实数k，使得关于x的方程（x2﹣1）2﹣|x2﹣1|+k=0的根的个数为2个、4个、5个、8个．则所有正确命题的序号为 ．

Answer 1

【答案】（1）（2）、（4）
【解析】解：对于（1），∵|f（x1）+f（x2）|≥|g（x1）+g（x2）|恒成立，
令x2=﹣x1 ， 则|f（x1）+f（﹣x1）|≥|g（x1）+g（﹣x1）|恒成立，
∵f（x）是奇函数，
∴|f（x1）﹣f（x1）|≥|g（x1）+g（﹣x1）|恒成立，
∴g（x1）+g（﹣x1）=0，
∴g（﹣x1）=﹣g（x1），
∴g（x）是奇函数，（1）正确；
对于（2），设x1＜x2 ，
∵f（x）是R上的增函数，
∴f（x1）＜f（x2），
∵|f（x1）﹣f（x2）|＞|g（x1）﹣g（x2）|恒成立，
∴f（x1）﹣f（x2）＜g（x1）﹣g（x2）＜f（x2）﹣f（x1），
∴h（x1）﹣h（x2）=f（x1）﹣f（x2）+g（x1）﹣g（x2）＜f（x1）﹣f（x2）+f（x2）﹣f（x1），
∴h（x1）﹣h（x2）＜0，
∴函数h（x）=f（x）+g（x）在R上是增函数，（2）正确；
对于（3），①当a＞1时，函数f（x）= 在[0，2]上的最大值为f（1）=a，最小值为f（0）=1或f（2）=a﹣2；
当a﹣1= 时，解得a= ，此时f（2）= ＞1，满足题意，
当a﹣（a﹣2）=0时，2=0不满足题意，∴a= ；
②当0＜a＜1时，在[0，1]上，f（x）=ax是减函数；在（1，2]上，f（x）=﹣x+a是减函数，
∵f（0）=a0=1＞﹣1+a，∴函数的最大值为f（0）=1；
而f（2）=﹣2+a＜﹣1+a=f（1），所以函数的最小值为f（2）=﹣2+a，
因此，﹣2+a+ =1，解得a= ∈（0，1）符合题意；
综上，实数a的取值集合为{ ， }，（3）错误；
对于（4），关于x的方程（x2﹣1）2﹣|x2﹣1|+k=0可化为（x2﹣1）2﹣（x2﹣1）+k=0（x≥1或x≤﹣1）（Ⅰ）
或（x2﹣1）2+（x2﹣1）+k=0（﹣1＜x＜1）（Ⅱ）
①当k= 时，方程（Ⅰ）有两个不同的实根± ，方程（Ⅱ）有两个不同的实根± ，
即原方程恰有4个不同的实根；
②当k=0时，原方程恰有5个不同的实根；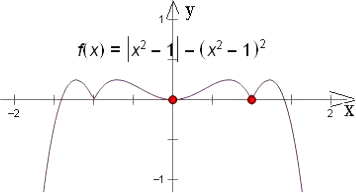

③当k= 时，方程（Ⅰ）的解为± ，± ，方程（Ⅱ）的解为± ，± ，
即原方程恰有8个不同的实根；
④当k=﹣2时，方程化为（|x2﹣1|+1）（|x2﹣1|﹣2）=0，
解得|x2﹣1|=2或|x2﹣1|=﹣1（不合题意，舍去）；
所以x2﹣1=±2，
解得x2﹣1=2，
即x=± ，方程有2个实数根；
所以存在不同的实数k，使得关于x的方程（x2﹣1）2﹣|x2﹣1|+k=0的根的个数为2个、4个、5个、8个，
命题（4）正确；
综上，正确的命题是（1）、（2）、（4）．
所以答案是：（1）（2）、（4）．
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较，以及对函数的奇偶性的理解，了解偶函数的图象关于y轴对称；奇函数的图象关于原点对称．