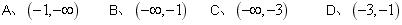题目内容
(1)当
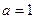 时, 求
时, 求 的单调区间、极值;
的单调区间、极值;(2)求证:在(1)的条件下,
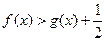 ;
;(3)是否存在实数
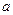 ,使
,使 的最小值是
的最小值是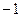 ,若存在,求出
,若存在,求出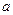 的值;若不存在,说明理由
的值;若不存在,说明理由(1)
 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e); 的极小值为
的极小值为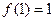
(3)
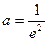
(1)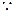 当
当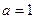 时,
时,
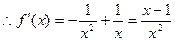 , 1分
, 1分
∴当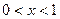 时,
时,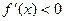 ,此时
,此时 单调递减
单调递减
当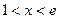 时,
时,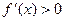 ,此时
,此时 单调递增 …………………………………3分
单调递增 …………………………………3分
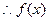 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e);
 的极小值为
的极小值为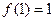 ………………………………………………4分
………………………………………………4分
(2)由(1)知 在
在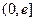 上的最小值为1, ……………………………………5分
上的最小值为1, ……………………………………5分
令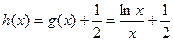 ,
,
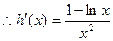 , ………………………6分
, ………………………6分
当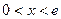 时,
时,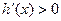 ,
,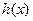 在
在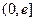 上单调递增 …………………………………7分
上单调递增 …………………………………7分
∴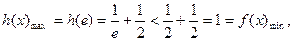 w
w
∴在(1)的条件下,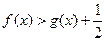 …………………………………………………8分
…………………………………………………8分
(1)假设存在实数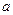 ,使
,使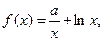 (
( )有最小值
)有最小值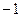 ,
,
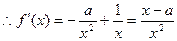 ……………………………………………………9分
……………………………………………………9分
①当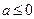 时,
时,
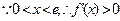 ,
,
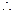
 在
在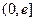 上单调递增,此时
上单调递增,此时 无最小值. …10分
无最小值. …10分
②当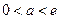 时,
时,
若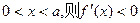 ,故
,故 在
在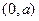 上单调递减,
上单调递减,
若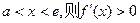 ,故
,故 在
在 上单调递增.
上单调递增.
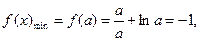 ,得
,得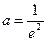 ,满足条件. ……………………………12分
,满足条件. ……………………………12分
③当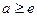 时,
时,
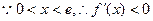 ,
,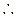
 在
在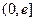 上单调递减,
上单调递减,
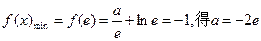 (舍去),
(舍去),
所以,此时 无最小值. ……13分
无最小值. ……13分 

综上,存在实数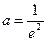 ,使得当
,使得当 时
时 的最小值是
的最小值是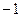 ……………………14分
……………………14分
(3)法二:假设存在实数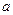 ,使
,使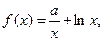
 的最小值是
的最小值是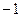 ,
,
故原问题等价于:不等式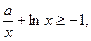 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
即不等式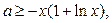 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.
设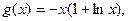 即
即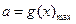 ,
, ………………10分
………………10分
又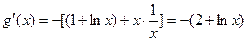 ……………………………11分
……………………………11分
令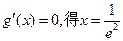
当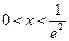 ,
,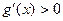 ,则
,则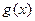 在
在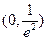 单调递增;
单调递增;
当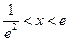 ,
,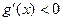 ,则
,则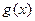 在
在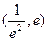 单调递减. ……………………13分
单调递减. ……………………13分
故当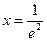 时,
时,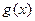 取得最大值,其值是
取得最大值,其值是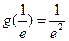 .
.
故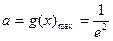
综上,存在实数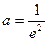 ,使得当
,使得当 时
时 的最小值是
的最小值是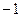 .……………………14分
.……………………14分
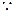 当
当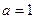 时,
时,
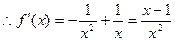 , 1分
, 1分∴当
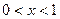 时,
时,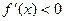 ,此时
,此时 单调递减
单调递减当
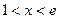 时,
时,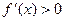 ,此时
,此时 单调递增 …………………………………3分
单调递增 …………………………………3分 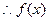 的的单调递减区间为(0,1);单调递增区间为(1,e);
的的单调递减区间为(0,1);单调递增区间为(1,e); 的极小值为
的极小值为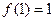 ………………………………………………4分
………………………………………………4分(2)由(1)知
 在
在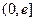 上的最小值为1, ……………………………………5分
上的最小值为1, ……………………………………5分令
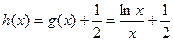 ,
,
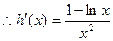 , ………………………6分
, ………………………6分当
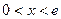 时,
时,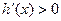 ,
,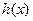 在
在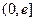 上单调递增 …………………………………7分
上单调递增 …………………………………7分∴
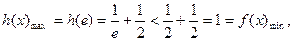 w
w∴在(1)的条件下,
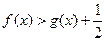 …………………………………………………8分
…………………………………………………8分(1)假设存在实数
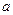 ,使
,使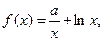 (
( )有最小值
)有最小值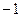 ,
,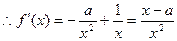 ……………………………………………………9分
……………………………………………………9分①当
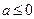 时,
时,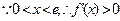 ,
,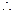
 在
在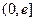 上单调递增,此时
上单调递增,此时 无最小值. …10分
无最小值. …10分 ②当
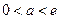 时,
时,若
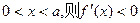 ,故
,故 在
在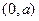 上单调递减,
上单调递减,若
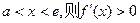 ,故
,故 在
在 上单调递增.
上单调递增.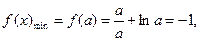 ,得
,得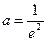 ,满足条件. ……………………………12分
,满足条件. ……………………………12分③当
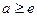 时,
时,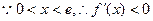 ,
,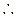
 在
在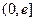 上单调递减,
上单调递减,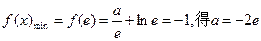 (舍去),
(舍去),所以,此时
 无最小值. ……13分
无最小值. ……13分 

综上,存在实数
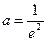 ,使得当
,使得当 时
时 的最小值是
的最小值是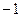 ……………………14分
……………………14分(3)法二:假设存在实数
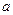 ,使
,使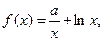
 的最小值是
的最小值是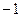 ,
,故原问题等价于:不等式
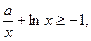 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.即不等式
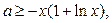 对
对 恒成立,求“等号”取得时实数a的值.
恒成立,求“等号”取得时实数a的值.设
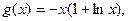 即
即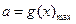 ,
, ………………10分
………………10分又
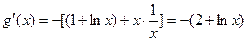 ……………………………11分
……………………………11分令
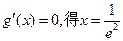
当
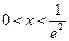 ,
,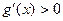 ,则
,则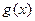 在
在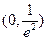 单调递增;
单调递增;当
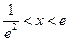 ,
,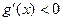 ,则
,则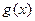 在
在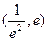 单调递减. ……………………13分
单调递减. ……………………13分故当
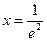 时,
时,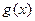 取得最大值,其值是
取得最大值,其值是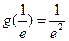 .
.故
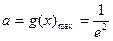
综上,存在实数
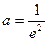 ,使得当
,使得当 时
时 的最小值是
的最小值是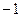 .……………………14分
.……………………14分
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
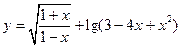 的定义域为
的定义域为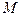 ,
,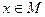 时,求
时,求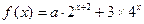
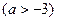 的最小值.
的最小值.
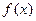 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;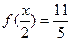 且
且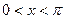 ,求
,求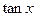 的值
的值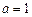 时,求所有使
时,求所有使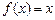 成立的
成立的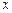 的值;
的值;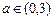 时,求函数
时,求函数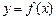 在闭区间
在闭区间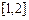 上的最小值;
上的最小值;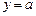 的交点个数
的交点个数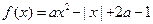
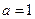 ,求
,求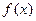 的单调区间;
的单调区间;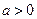 ,设
,设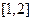 的最小值为
的最小值为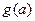 ,求
,求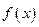 是定义在
是定义在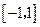 上的奇函数,且
上的奇函数,且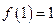 ,若
,若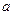 ,
,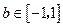 ,
,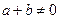 ,有
,有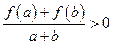 ,判断函数
,判断函数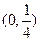 上为减函数的是( )
上为减函数的是( )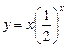 ;
;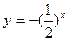 ;
;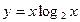 ;
;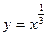
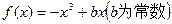 ,且
,且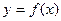 在区间(0,1)上单调递增,并且函数
在区间(0,1)上单调递增,并且函数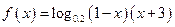 的递减区间是
的递减区间是