题目内容
【题目】已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴都交于正半轴,当直线
轴都交于正半轴,当直线![]() 与坐标轴围成的三角形面积取得最小值时,求:
与坐标轴围成的三角形面积取得最小值时,求:
(1)直线![]() 的方程;
的方程;
(2)直线l关于直线m:y=2x-1对称的直线方程.
【答案】(1)![]() ;(2)直线为x-3y+4=0.
;(2)直线为x-3y+4=0.
【解析】
(1)利用斜率设出直线方程,求出与x轴、y轴的交点坐标,计算三角形的面积,求出最小值以及对应的斜率k,写出直线方程;
(2)显然所求直线的斜率存在,利用对称关系列方程求出斜率和交点坐标,再写出所求的直线方程.
(1)由已知,直线![]() 的斜率存在,且小于0,
的斜率存在,且小于0,
设直线y-3=k(x-1),其中k<0
与x轴交于点![]() , 与y轴交于点(0,3-k),
, 与y轴交于点(0,3-k),
故![]() ,等号成立的条件是k=-3,
,等号成立的条件是k=-3,
相应地,![]() ;
;
(2)显然所求直线的斜率存在,设为k,
则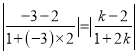 得
得![]()
又由![]() 得
得![]() 与m的交点为
与m的交点为![]() ,该点也在所求直线上,
,该点也在所求直线上,
故所求直线为x-3y+4=0;

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目