题目内容
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
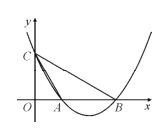
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求实数
,求实数![]() 的值;
的值;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时
面积的最大时![]() 的值.
的值.
【答案】(1)证明见解析;(2)①0,②2,![]() .
.
【解析】
(1)首先根据题中条件求出圆方程,再根据圆与直线的位置关系证明直线与圆相交;
(2)①利用圆与直线所交弦长和圆的半径求出参数![]() 即可,②根据弦长与点到直线距离公式列出
即可,②根据弦长与点到直线距离公式列出![]() 的面积公式,即可求出最大面积,再根据最大面积求出直线方程中的参数
的面积公式,即可求出最大面积,再根据最大面积求出直线方程中的参数![]() .
.
(1)∵![]() ,
,![]() ,
,
∴![]() 的垂直平分线为
的垂直平分线为![]() ,
,
联立![]() 得圆心坐标
得圆心坐标![]() ,
,
∴圆的方程为![]() ,
,
∵圆![]() 过点
过点![]() ,
,
∴![]() ,
,
得到圆的方程![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
联立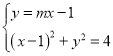 ,
,
得![]() ,
,
∴![]() ,
,
∴直线![]() 与圆
与圆![]() 相交;
相交;
(2)记圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
①∵![]() ,
,
解得![]() ,
,
∴![]() ,
,
解得![]() ,
,
②![]() ,
,
当![]() 时,三角形面积的最大值为2,
时,三角形面积的最大值为2,
此时![]() ,
,
解得![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目