题目内容
【题目】已知实数![]() 满足:
满足:![]() ,且
,且![]() 其中
其中![]() ,则以向量
,则以向量![]() 为法向量的直线的倾斜角的取值范围是__________.
为法向量的直线的倾斜角的取值范围是__________.
【答案】![]()
【解析】
由已知可得,向量![]() =(a1,b1)的终点在直线x﹣y+1=0上,向量
=(a1,b1)的终点在直线x﹣y+1=0上,向量![]() =(a2,b2)的终点在直线x﹣y+1=0上,把已知等式变形求得,
=(a2,b2)的终点在直线x﹣y+1=0上,把已知等式变形求得,![]() ,
,![]() 的夹角为
的夹角为![]() ,再由a1>a2可得A的位置,数形结合可得以向量(a1,b1)为法向量的直线的倾斜角的取值范围.
,再由a1>a2可得A的位置,数形结合可得以向量(a1,b1)为法向量的直线的倾斜角的取值范围.
解:向量![]() =(a1,b1)的终点在直线x﹣y+1=0上,向量
=(a1,b1)的终点在直线x﹣y+1=0上,向量![]() =(a2,b2)的终点在直线x﹣y+1=0上,
=(a2,b2)的终点在直线x﹣y+1=0上,
由![]() 得
得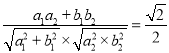 ,
,
即向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,
,
又a1>a2,可得点A在曲线x﹣y+1=0(x>﹣1)上,
如图,
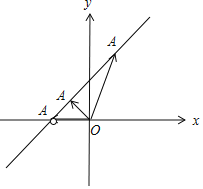
则OA所在直线的斜率为(﹣∞,0)∪(1,+∞),
∴以向量(a1,b1)为法向量的直线的斜率为(0,+∞)∪(﹣1,0),
倾斜角的范围为(0,![]() )∪(
)∪(![]() ,π),
,π),
当A为(0,1)时,以向量(a1,b1)为法向量的直线的倾斜角为0.
∴以向量(a1,b1)为法向量的直线的倾斜角的范围为[0,![]() )∪(
)∪(![]() ,π),
,π),
故答案为: [0,![]() )∪(
)∪(![]() ,π).
,π).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目