题目内容
【题目】如图，在三棱柱ABC﹣A1B1C1中，点D是A1B的中点，点E是B1C1的中点．
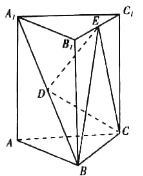
（1）求证：DE∥平面ACC1A1；
（2）若△ABC的面积为
，三棱柱ABC﹣A1B1C1的高为3，求三棱锥D﹣BCE的体积．
【答案】（1）见解析； （2）
.
【解析】
（1）连接AB1，AC1，即可得DE∥AC1．可证明DE∥平面ACC1A1；
（2）由S
可得三棱锥D﹣BCE的体积V=
代值计算即可得解.
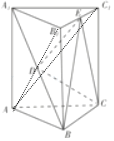
证明：（1）连接AB1，AC1，
∵点D是A1B的中点，点E是B1C1的中点．∴在△AB1C1中，DE是中位线，即可得DE∥AC1．
∵DE平面ACC1A1，AC1平面ACC1A1；
∴DE∥平面ACC1A1；
（2）∵点D是A1B的中点，∴D到面BCE的距离是A到面BCE的一半．
又S
∴三棱锥D﹣BCE的体积V=
=．
练习册系列答案
相关题目
【题目】某公司的新能源产品上市后在国内外同时销售，已知第一批产品上市销售40天内全部售完，该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查，如图所示，其中图①中的折线表示的是国外市场的日销售量与上市时间的关系；图②中的抛物线表示的是国内市场的日销售量与上市时间的关系；下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系．
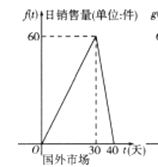图① 图②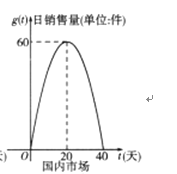
第t天产品广告费用（单位：万元） | 每件产品成本（单位：万元） | 每件产品销售价格（单位：万元） | |
|
| 3 | 6 |
| 10 | 3 | 5 |
(1)分别写出国外市场的日销售量
、国内市场的日销售量
与产品上市时间t的函数关系式；
(2)产品上市后的哪几天，这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价－单件产品成本)×日销售量－当天广告费用，
)
