Question

【题目】设Sn是数列{an}的前n项和，且a1=﹣1， =Sn ， 求数列{an}的前n项和Sn= ， 通项公式an= ．

Answer 1

【答案】﹣ ；
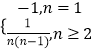
【解析】解：由Sn是数列{an}的前n项和，且a1=﹣1， =Sn ， ∴an+1=SnSn+1 ，
∴Sn+1﹣Sn=Sn+1Sn ， 两边同除以Sn+1Sn ，
∴ ﹣ =1，即 ﹣ =﹣1，
=﹣1，
∴{ }是首项为﹣1，公差为﹣1的等差数列，
∴ =﹣1+（n﹣1）×（﹣1）=﹣n．
∴Sn=﹣ ，
当n=1时，a1=S1=﹣1，
n≥2时，an=Sn﹣Sn﹣1=﹣ + = ．
∴an= ．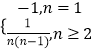
故答案为：﹣ ， ．
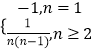由题意可知：an+1=SnSn+1 ， 即Sn+1﹣Sn=Sn+1Sn ， 两边同除以Sn+1Sn ， 整理得： ﹣ =﹣1，则{ }是首项为﹣1，公差为﹣1的等差数列，由等差数列通项公式可知： =﹣1+（n﹣1）×（﹣1）=﹣n，则Sn=﹣ ；由当n=1时，a1=S1=﹣1，n≥2时，an=Sn﹣Sn﹣1= ．