题目内容
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 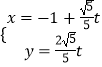 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
【答案】解:(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρcosθ, 又x2+y2=ρ2 , x=ρcosθ,
∴曲线C的直角坐标方程为x2+y2﹣2x=0.
(Ⅱ)将直线l的参数方程化为直角坐标方程,得y=2x+2,
令x=0得y=2,即M点的坐标为(0,2).
又曲线C为圆,圆C的圆心坐标为(1,0),半径r=1,
则|MC|= ![]() ,
,
|MN|≤|MC|+r= ![]() +1.
+1.
∴MN的最大值为 ![]() +1
+1
【解析】(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρcosθ,利用x2+y2=ρ2 , x=ρcosθ,即可得出;(Ⅱ)求出点M与圆心的距离d,即可得出最小值.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.

【题目】近年来,手机已经成为人们日常生活中不可缺少的产品,手机的功能也日趋完善,已延伸到了各个领域,如拍照,聊天,阅读,缴费,购物,理财,娱乐,办公等等,手机的价格差距也很大,为分析人们购买手机的消费情况,现对某小区随机抽取了200人进行手机价格的调查,统计如下:
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
(Ⅰ)完成关于人们使用手机的价格和年龄的2×2列联表,再判断能否在犯错误的概率不超过0.025的前提下,认为人们使用手机的价格和年龄有关?
(Ⅱ)从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况,设3人中年龄在45岁及以下的人数为随机变量X,求随机变量X的分布列及数学期望.
附K2= ![]()
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |