��Ŀ����
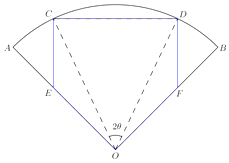
����Ŀ���ס�����λͬѧ�μ���ѧ�Ļ�֪ʶ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴβ��Գɼ��������ȡ8�Σ���¼���£� �ף�8281797895889384
�ң�9295807583809085
�����þ�Ҷͼ��ʾ���������ݣ�
������Ҫ����ѡ��һ�˲μ���ʽ������������ȡ���������ݷ���������Ϊѡ����λͬѧ�μӽ�Ϊ���ʣ���˵�����ɣ�
�������Լ�ͬѧ�ڽ���3�β��Գɼ�����Ԥ�⣬����3�γɼ��и���80�ֵĴ���Ϊ�Σ�����8�γɼ��и���80�ֵ�Ƶ����Ϊ���ʣ�����εķֲ��м���ѧ����E�Σ�
���𰸡��⣺����������Ҷͼ���£� �����ɼײ����ȽϺ��ʣ��������£� ![]() ��
�� ![]() ��
�� ![]() ��88��85��2+
��88��85��2+
��93��85��2+��95��85��2]=35.5�� ![]() ��90��85��2+��92��85��2+��95��85��2]=41��
��90��85��2+��92��85��2+��95��85��2]=41��
��Ϊ ![]() =
= ![]() ��
�� ![]() ��
��
���ԣ��ijɼ����ȶ����ɼײ����ȽϺ��ʣ�
ע����С��Ľ��ۼ����ɾ���Ψһ����������ܴ�ͳ��ѧ�ĽǶȷ������������������ش�ͬ�����֣���
���Ҳ����ȽϺ��ʣ��������£�
��ͳ�ƵĽǶȿ������8��5�֣����ϣ���85�֣���Ƶ��Ϊ ![]() ��
��
�һ��8��5�֣����ϣ���85�֣���Ƶ��Ϊ ![]() ��
��
��Ϊf2��f1 �� �������Ҳ����ȽϺ��ʣ�
���ǡ���ͬѧ��һ����ѧ�����гɼ�����8��0�֣���Ϊ�¼�A�� ![]() ��
��
��������εĿ���ȡֵΪ0��1��2��3���� ![]() ��
��
�� ![]() ��k=0��1��2��3��
��k=0��1��2��3��
���Ա����εķֲ���Ϊ��
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() ��
��
���� ![]() ����
����
������������������Ҷͼ����II������ƽ����������ļ��㹫ʽ���ɵó������ǡ���ͬѧ��һ����ѧ�����гɼ�����8��0�֣���Ϊ�¼�A�� ![]() ����������εĿ���ȡֵΪ0��1��2��3����
����������εĿ���ȡֵΪ0��1��2��3���� ![]() ���ɵ�
���ɵ� ![]() ��k=0��1��2��3��
��k=0��1��2��3��
�����㾫����������Ҫ�����˾�Ҷͼ����ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ���վ�Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��٣����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮