题目内容
【题目】已知椭圆 C: ![]() =1( a>b>0)经过点 (1,
=1( a>b>0)经过点 (1, ![]() ),离心率为
),离心率为 ![]() ,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
,点 A 为椭圆 C 的右顶点,直线 l 与椭圆相交于不同于点 A 的两个点P (x1 , y1),Q (x2 , y2).
(Ⅰ)求椭圆 C 的标准方程;
(Ⅱ)当 ![]()
![]() =0 时,求△OPQ 面积的最大值;
=0 时,求△OPQ 面积的最大值;
(Ⅲ)若直线 l 的斜率为 2,求证:△APQ 的外接圆恒过一个异于点 A 的定点.
【答案】解:(Ⅰ)由椭圆的离心率e= ![]() =
= ![]() ,即c2=
,即c2= ![]() a2 , 即b2=a2﹣c2=
a2 , 即b2=a2﹣c2= ![]() a2 , a2=4b2 ,
a2 , a2=4b2 ,
将点 (1, ![]() )代入椭圆方程
)代入椭圆方程 ![]() ,即
,即 ![]() ,解得:b2=1,
,解得:b2=1,
∴a2=4,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)当直线l的斜率不存在时,设l:x=m,代入椭圆方程 ![]() ,
,
P(m, ![]() ),Q(m,﹣
),Q(m,﹣ ![]() ),
),
由 ![]()
![]() =0,(m﹣2)2﹣(1﹣
=0,(m﹣2)2﹣(1﹣ ![]() )=0,解得:m=
)=0,解得:m= ![]() ,m=2(舍去),
,m=2(舍去),
此时丨PQ丨= ![]() ,△OPQ的面积为
,△OPQ的面积为 ![]() ,
,
当直线l的斜率存在时,设l:y=kx+m,代入椭圆方程,(4k2+1)x2+8kmx+4(m2﹣1)=0,
由△>0,则4k2﹣m2+1>0,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由 ![]()
![]() =0,
=0,
(x1﹣2)(x2﹣2)+y1y2=(k2+1)x1x2+(km﹣2)(x1+x2)+m2+4=0,
代入求得12k2+5m2+16km=0,
即m=﹣ ![]() k,m=﹣2k,(此时直线l过点A,舍去),
k,m=﹣2k,(此时直线l过点A,舍去),
丨PQ丨= ![]()
![]() =
= ![]()
![]() ,
,
点O到直线l的距离d= ![]() ,
,
△OPQ的面积为 ![]() ,将m=﹣
,将m=﹣ ![]() k代入,
k代入,![]() ×
× 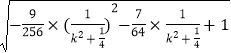 <
< ![]() ,
,
△OPQ 面积的最大值 ![]() ;
;
(Ⅲ)证明:设直线y=2x+m,代入椭圆方程,整理得:17x2+16mx+4(m2﹣1)=0,
设△△APQ的外接圆方程x2+y2+Dx+Ey+F=0,
联立直线l的方程,5x2+(4m+D+2E)x+(m2+mE+F)=0,
代入可知 ![]() =
= ![]() =
= ![]() ,
,
由外接圆过点A(2,0),则2D+F=﹣4,
从而可得关于D,E,F的三元一次方程组,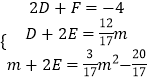 ,解得:
,解得: 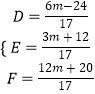 ,
,
代入椭圆方程,整理得:(x2+y2﹣ ![]() x+
x+ ![]() y﹣
y﹣ ![]() )+
)+ ![]() (2x+y﹣4)=0,
(2x+y﹣4)=0,
∴ 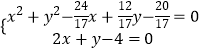 ,解得:
,解得: 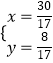 ,或
,或 ![]() ,
,
△APQ 的外接圆恒过一个异于点A的定点( ![]() ,
, ![]() )
)
【解析】(Ⅰ)由椭圆的离心率,求得a和b的关系,将P代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)当斜率不存在时,求P和Q点坐标,由 ![]()
![]() =0,求得m的值,求得丨PQ丨求得,△OPQ的面积,当斜率存在时,设直线l方程,代入椭圆方程,利用韦达定理及弦长公式及三角形的面积公式,即可求得△OPQ 面积的最大值;(Ⅲ)设直线y=2x+m,代入椭圆方程,设外接圆的方程,联立直线l的方程,将A代入外接圆方程,联立方程,即可求得△APQ 的外接圆恒过一个异于点 A 的定点.
=0,求得m的值,求得丨PQ丨求得,△OPQ的面积,当斜率存在时,设直线l方程,代入椭圆方程,利用韦达定理及弦长公式及三角形的面积公式,即可求得△OPQ 面积的最大值;(Ⅲ)设直线y=2x+m,代入椭圆方程,设外接圆的方程,联立直线l的方程,将A代入外接圆方程,联立方程,即可求得△APQ 的外接圆恒过一个异于点 A 的定点.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.