题目内容
19.设[x]表示不超过实数x的最大整数,如[2.6]=2,[-2.6]=-3,设g(x)=$\frac{{a}^{x}}{{a}^{x}+1}$(a>0且a≠1),那么函数f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]的值域为( )| A. | {-1,0,1} | B. | {0,1} | C. | {1,-1} | D. | {-1,0} |
分析 由已知可得g(x)+g(-x)=1,且g(x),g(-x)=1∈(0,1),进而分类讨论,求出函数f(x)的值,最后综合讨论结果,可得答案.
解答 解:∵g(x)=$\frac{{a}^{x}}{{a}^{x}+1}$(a>0且a≠1),
∴g(-x)=$\frac{{a}^{-x}}{{a}^{-x}+1}$=$\frac{1}{{a}^{x}+1}$(a>0且a≠1),
故g(x)+g(-x)=1,
又由g(x)=$\frac{{a}^{x}}{{a}^{x}+1}$=1-$\frac{1}{{a}^{x}+1}$∈(0,1),
故当g(x)∈(0,$\frac{1}{2}$)时,g(-x)∈($\frac{1}{2}$,1)时,
f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]=-1+0=-1,
当g(x)=g(-x)=$\frac{1}{2}$时,
f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]=0+0=0,
当g(x)∈($\frac{1}{2}$,1)时,g(-x)∈(0,$\frac{1}{2}$),
f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]=0+(-1)=-1,
综上所述函数f(x)=[g(x)-$\frac{1}{2}$]+[g(-x)-$\frac{1}{2}$]的值域为{-1,0},
故选:D.
点评 本题考查的知识点是函数的值域,指数函数的图象和性质,其中根据已知分析出g(x)+g(-x)=1,且g(x),g(-x)=1∈(0,1),是解答的关键.

练习册系列答案
相关题目
14.由一排编号为1至7的七个座位连成一排,现有2名语文老师和2名数学老师共4人就坐,要求同一学科的老师不能相邻,有多少种不同的坐法( )
| A. | 400 | B. | 330 | C. | 440 | D. | 324 |
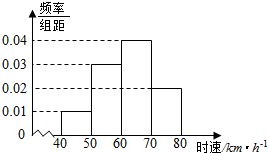 200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.
200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.